Blog
-
Bounding the largest eigenvalue of the random features gram matrix
\[\def\sign{\operatorname{sign}}
\def\qed{\Box}
\def\im{\operatorname{im}}
\def\grad{\operatorname{grad}}
\def\curl{\operatorname{curl}}
\def\div{\operatorname{div}}
\def\dim{\operatorname{dim}}
\def\X{\mathcal X}
\def\Y{\mathcal Y}
\def\C{\mathcal C}
\def\M{\mathcal M}
\def\Xstar{\X^\star}
\def\Ystar{\Y^\star}
\def\Astar{A^\star}
\def\BX{\mathbb B_{\X}}
\def\BXstar{\mathbb B_{\Xstar}}
\def\Xss{\X^{\star\star}}
\def\Yss{\Y^{\star\star}}
\def\gss{g^{\star\star}}
\def\fss{f^{\star\star}}
\def\fstar{f^\star}
\def\gstar{g^\star}
\def\xstar{x^\star}
\def\ystar{y^\star}
\def\opt{\operatorname{opt}}
\def\dom{\operatorname{dom}}
\def\conv{\operatorname{conv}}
\def\epi{\operatorname{epi}}
\def\iff{\;\operatorname{iff}\;}
\def\st{\;\operatorname{s.t}\;}
\def\softmax{\operatorname{softmax}}
\def\kl{\operatorname{KL}}
\def\tv{\operatorname{TV}}
\def\div{\operatorname{div}}
\def\inte{\operatorname{int}}
\def\ball{\mathbb B}
\def\card{\operatorname{card}}
\def\enet{\mathcal N_\epsilon}
\def\bP{\mathbb P}\]
-
A criminal's view of random matrix theory
\[\def\sign{\operatorname{sign}}
\def\qed{\Box}
\def\im{\operatorname{im}}
\def\grad{\operatorname{grad}}
\def\curl{\operatorname{curl}}
\def\div{\operatorname{div}}
\def\dim{\operatorname{dim}}
\def\X{\mathcal X}
\def\Y{\mathcal Y}
\def\C{\mathcal C}
\def\M{\mathcal M}
\def\Xstar{\X^\star}
\def\Ystar{\Y^\star}
\def\Astar{A^\star}
\def\BX{\mathbb B_{\X}}
\def\BXstar{\mathbb B_{\Xstar}}
\def\Xss{\X^{\star\star}}
\def\Yss{\Y^{\star\star}}
\def\gss{g^{\star\star}}
\def\fss{f^{\star\star}}
\def\fstar{f^\star}
\def\gstar{g^\star}
\def\xstar{x^\star}
\def\ystar{y^\star}
\def\opt{\operatorname{opt}}
\def\dom{\operatorname{dom}}
\def\conv{\operatorname{conv}}
\def\epi{\operatorname{epi}}
\def\iff{\;\operatorname{iff}\;}
\def\st{\;\operatorname{s.t}\;}
\def\softmax{\operatorname{softmax}}
\def\kl{\operatorname{KL}}
\def\tv{\operatorname{TV}}
\def\div{\operatorname{div}}
\def\inte{\operatorname{int}}
\def\ball{\mathbb B}
\def\card{\operatorname{card}}
\def\enet{\mathcal N_\epsilon}
\def\bP{\mathbb P}\]
-
Fenchel-Rockafellar duality theorem, one ring to rule'em all! - Part 2
\[\def\sign{\operatorname{sign}}
\def\qed{\Box}
\def\im{\operatorname{im}}
\def\grad{\operatorname{grad}}
\def\curl{\operatorname{curl}}
\def\div{\operatorname{div}}
\def\dim{\operatorname{dim}}
\def\dist{\operatorname{dist}}
\def\X{\mathcal X}
\def\Z{\mathcal Z}
\def\Y{\mathcal Y}
\def\Zstar{\Z^\star}
\def\Vstar{V^\star}
\def\vstar{v^\star}
\def\ustar{u^\star}
\def\Kplus{K^+}
\def\C{\mathcal C}
\def\M{\mathcal M}
\def\Xstar{\X^\star}
\def\Ystar{\Y^\star}
\def\Astar{A^\star}
\def\Fstar{F^\star}
\def\BX{\mathbb B_{\X}}
\def\BXstar{\mathbb B_{\Xstar}}
\def\Xss{\X^{\star\star}}
\def\Yss{\Y^{\star\star}}
\def\gss{g^{\star\star}}
\def\fss{f^{\star\star}}
\def\fstar{f^\star}
\def\gstar{g^\star}
\def\xstar{x^\star}
\def\ystar{y^\star}
\def\zstar{z^\star}
\def\opt{\operatorname{opt}}
\def\dom{\operatorname{dom}}
\def\conv{\operatorname{conv}}
\def\epi{\operatorname{epi}}
\def\iff{\;\operatorname{iff}\;}
\def\st{\;\operatorname{s.t}\;}
\def\softmax{\operatorname{softmax}}
\def\kl{\operatorname{KL}}
\def\tv{\operatorname{TV}}
\def\div{\operatorname{div}}
\def\inte{\operatorname{int}}
\def\dim{\operatorname{dim}}\]
-
Fenchel-Rockafellar duality theorem, one ring to rule'em all! - Part 1
\[\def\sign{\operatorname{sign}}
\def\qed{\Box}
\def\im{\operatorname{im}}
\def\grad{\operatorname{grad}}
\def\curl{\operatorname{curl}}
\def\div{\operatorname{div}}
\def\dim{\operatorname{dim}}
\def\X{\mathcal X}
\def\Y{\mathcal Y}
\def\C{\mathcal C}
\def\M{\mathcal M}
\def\Xstar{\X^\star}
\def\Ystar{\Y^\star}
\def\Astar{A^\star}
\def\BX{\mathbb B_{\X}}
\def\BXstar{\mathbb B_{\Xstar}}
\def\Xss{\X^{\star\star}}
\def\Yss{\Y^{\star\star}}
\def\gss{g^{\star\star}}
\def\fss{f^{\star\star}}
\def\fstar{f^\star}
\def\gstar{g^\star}
\def\xstar{x^\star}
\def\ystar{y^\star}
\def\opt{\operatorname{opt}}
\def\dom{\operatorname{dom}}
\def\conv{\operatorname{conv}}
\def\epi{\operatorname{epi}}
\def\iff{\;\operatorname{iff}\;}
\def\st{\;\operatorname{s.t}\;}
\def\softmax{\operatorname{softmax}}
\def\kl{\operatorname{KL}}
\def\tv{\operatorname{TV}}
\def\div{\operatorname{div}}
\def\inte{\operatorname{int}}\]
-
Discrete de Rham-Hodge cohomology theory: application to game theory and statistical ranking (Part I)
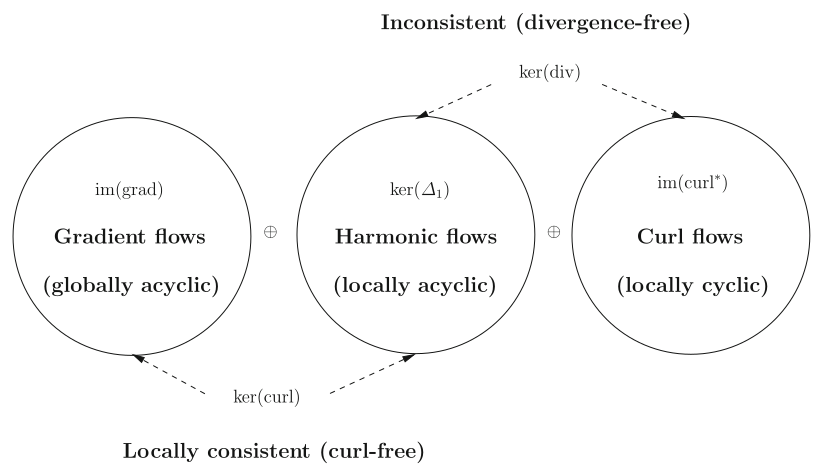
Cohomology is a central concept in algebraic topology and geometry. Oddly enough, this theory applies to certain concrete problems arising in machine learning (e.g globally consistent ranking of items in an online shop like Amazon or NetFlix) and game theory (e.g approximating multi-player non-cooperative games with potential games, in view of computing approximate Nash equilibria of the former).
-
Beware of standardizing data before running PCA!
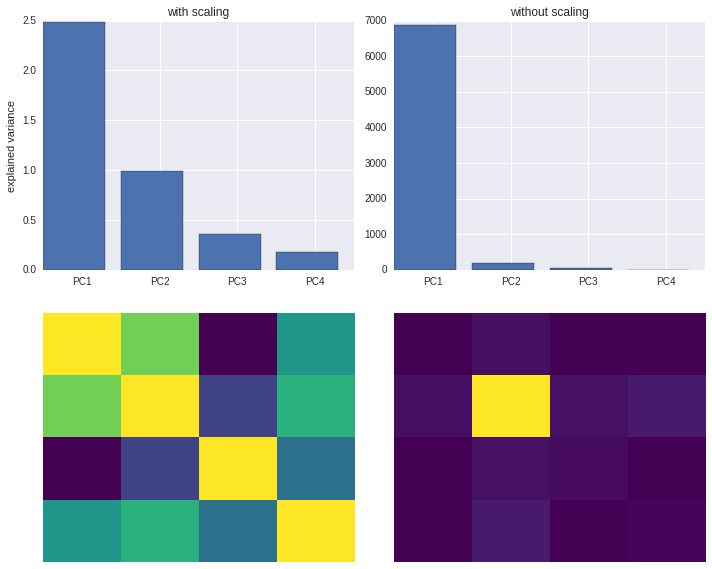
Standardization is important in PCA since the latter is a variance maximizing exercise. It projects your original data onto directions which maximize the variance. If your features have different scales, then this projection may get screwed!
-
Variational auto-encoder for "Frey faces" using keras
In this post, I’ll demo variational auto-encoders [Kingma et al. 2014] on the “Frey faces” dataset, using the keras deep-learning Python library.
-
Computing Nash-equilibria in incomplete information games
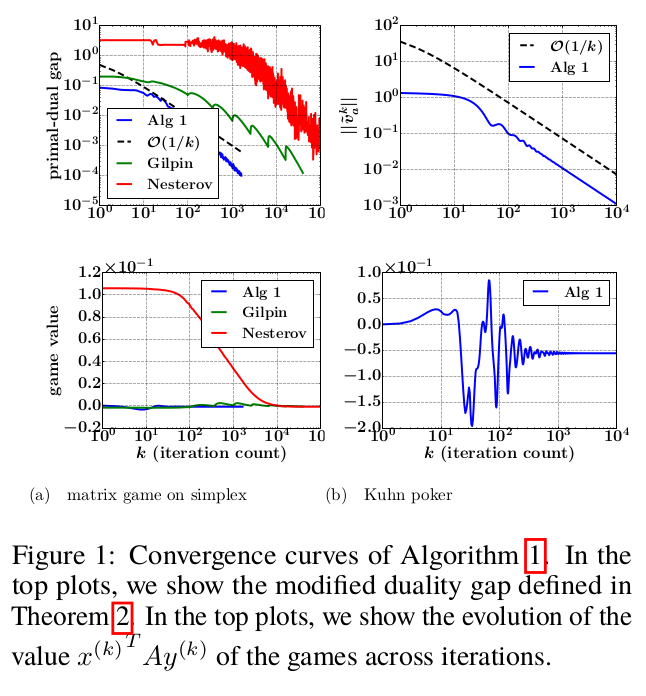
In our OPT2016 NIPS workshop paper, we propose a simple projection-free primal-dual algorithm for computing approxi- mate Nash-equilibria in two-person zero-sum sequential games with incomplete information and perfect recall (like Texas Hold’em Poker). Our algorithm is numer- ically stable, performs only basic iterations (i.e matvec multiplications, clipping, etc., and no calls to external first-order oracles, no matrix inversions, etc.), and is applicable to a broad class of two-person zero-sum games including simultaneous games and sequential games with incomplete information and perfect recall. The ap- plicability to the latter kind of games is thanks to the sequence-form representation which allows one to encode such a game as a matrix game with convex polytopial strategy profiles. We prove that the number of iterations needed to produce a Nash- equilibrium with a given precision is inversely proportional to the precision. We present experimental results on matrix games on simplexes and Kuhn Poker.
-
Learning brain regions from large-scale online structured sparse DL
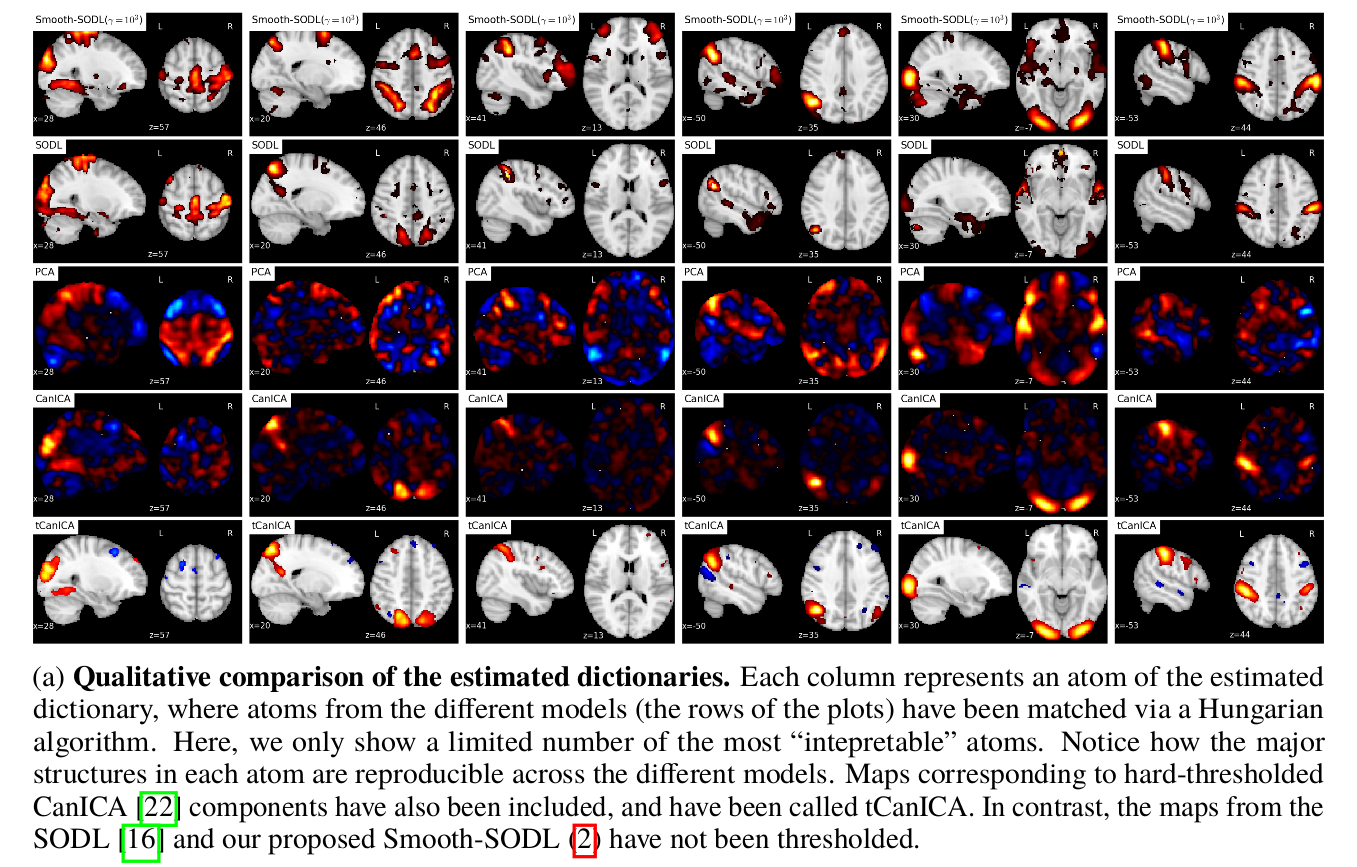
In our NIPS 2016, paper, we propose a multivariate online dictionary-learning method for obtaining decompositions of brain images with structured and sparse components (aka atoms). Sparsity is to be understood in the usual sense: the dictionary atoms are constrained to contain mostly zeros. This is imposed via an L1-norm constraint. By “structured”, we mean that the atoms are piece-wise smooth and compact, thus making up blobs, as opposed to scattered patterns of activation. We propose to use a Sobolev (Laplacian) penalty to impose this type of structure. Combining the two penalties, we obtain decompositions that properly delineate brain structures from functional images. This non-trivially extends the online dictionary-learning work of Mairal et al. (2010), at the price of only a factor of 2 or 3 on the overall running time. Just like the Mairal et al. (2010) reference method, the online nature of our proposed algorithm allows it to scale to arbitrarily sized datasets. Experiments on brain data show that our proposed method extracts structured and denoised dictionaries that are more intepretable and better capture inter-subject variability in small medium, and large-scale regimes alike, compared to state-of-the-art models.
subscribe via RSS