\[\def\sign{\operatorname{sign}} \def\qed{\Box} \def\im{\operatorname{im}} \def\grad{\operatorname{grad}} \def\curl{\operatorname{curl}} \def\div{\operatorname{div}} \def\dim{\operatorname{dim}} \def\X{\mathcal X} \def\Y{\mathcal Y} \def\C{\mathcal C} \def\M{\mathcal M} \def\Xstar{\X^\star} \def\Ystar{\Y^\star} \def\Astar{A^\star} \def\BX{\mathbb B_{\X}} \def\BXstar{\mathbb B_{\Xstar}} \def\Xss{\X^{\star\star}} \def\Yss{\Y^{\star\star}} \def\gss{g^{\star\star}} \def\fss{f^{\star\star}} \def\fstar{f^\star} \def\gstar{g^\star} \def\xstar{x^\star} \def\ystar{y^\star} \def\opt{\operatorname{opt}} \def\dom{\operatorname{dom}} \def\conv{\operatorname{conv}} \def\epi{\operatorname{epi}} \def\iff{\;\operatorname{iff}\;} \def\st{\;\operatorname{s.t}\;} \def\softmax{\operatorname{softmax}} \def\kl{\operatorname{KL}} \def\tv{\operatorname{TV}} \def\div{\operatorname{div}} \def\inte{\operatorname{int}}\]

I – Introduction

The Fenchel-Rockafellar duality theorem (FRDT), named after mathematicians Werner Fenchel and R.T Rockafellar, is perhaps the most powerful tool in all of convex analysis. The theorem arises from studying the optimization problem

\[p = \inf_{x \in \X}\;f(Ax) + g(x), \tag{P}\]

where $A: \X \rightarrow \Y$ is a “bounded” linear operator between “Banach spaces” $\X$ and $\Y$, and $g :\X \rightarrow (-\infty, +\infty]$ and $f:\Y \rightarrow (-\infty, +\infty]$ are functions. $\Astar: \Ystar \rightarrow \Xstar$ is the “adjoint” of $A$. FRDT is a result on the equivalence (under certain technical conditions) of the above so-called primal problem, with its dual problem given below

\[d = \sup_{\ystar \in \Ystar}\;-\fstar(-\ystar) - \gstar(\Astar\ystar). \tag{D}\]

Here $\Ystar$ is the “topological dual” of the Banach space $\Y$ and $\fstar$ denotes “convex / Fenchel conjugation”, a kind of Fourier transform, but for the subject of convex analysis! The precise meaning of these technical concepts will become clear later.

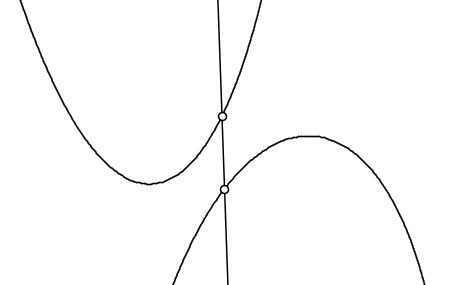
Fig. 1. (Figure courtesy of Wikipedia “In the following figure, the minimization problem on the left side of the equation is illustrated. One seeks to vary x such that the vertical distance between the convex and concave curves at x is as small as possible. The position of the vertical line in the figure is the (approximate) optimum.”)

Example: The Lasso. For example, consider the L1-penalized least-squares regression problem

\[\inf_{x \in \mathbb R^p}\|Ax-b\|_2^2 + \lambda\|x\|_1,\]

where $A \in \mathbb R^{n \times p}$ is the design matrix (one row per sample) and $b \in \mathbb R^n$ is the vector of prediction targets (one entry per sample), $\lambda > 0$ is a regularization parameter, and $x \in \mathbb R^p$ is the sought-for regression coefficients. The above problem can be succinctly rewritten in the form (P) with $f(y) := \frac{1}{2}\|y-b\|_2^2$ and $g(x) := \lambda \|x\|_1.$ We will return to this problem before the end of the exposition.

Preface to The Force. FRDT is so powerful that it can can be used to prove the Robinstein-Kantorovich duality formula (RKDF) (optimal transport) in 2 lines or so! The world in which FRDT lives is semantically more mature than the usual notions of Lagrange duality, slack variables, and all the other assorted objects manipulated in linear programming, for example. However, it seems FRDT is still not known to the general technical public (ML people, etc.). My plan is to develop the theory, bottom-up, show-case a few practical and conceptual applications.

Why Banach spaces ? This is not Abstract Nonsense! To present FRDT in full generality, the kind of generality which allows it to be used to prove the RKDF of optimal transport, one needs to work in Banach spaces, not just Hilbert spaces, or worst still, some “$\mathbb R^n$”. The good news is that “Banach spaces” (named after Polish mathematician Stefan Banach) are simpler than they sound. It’s all about norms, transposes of matrices (or more formally “adjoints” of bounded linear operators), etc.

I.1 Plan

The exposition will be split into different parts, delivering by means of various blogposts (roughly two or threw max).

In this first blog-post, I’ll start off with some central concepts in convex analysis (Banach spaces, dual spaces, Fenchel conjugates, subdiffirentials, etc.).
Subsequent blogposts will dive into the meat of the FRDT.
Several worked examples and exercises will be scattered in the middle of each blogpost. Readers are strongly advised to think about the exercises. Questions / hints may be asked in the comments section (at the end of each blogpost). I’ll try to be as responsive as possible.

Now that all the boring stuff is out of the way, let’s get down to business.

I.2 – Exercises

Exercise 1.2.1. Prove that $\inf_x\;\sup_y\; \Phi(x, y) \ge \sup_y\;\inf_x\; \Phi(x, y)$.

Exercise 1.2.2. Prove that $\sup_{a,b}u(a) + u(b) = \sup_a u(a) + \sup_b u(b)$.

II – Preliminaries on convex analysis

II.1 Banach spaces, linear operators, cones, convexity

II.1.1 – Banach spaces, their duals, cones, and bounded linear operators

Given a (real) Banach space $\X=(\X,\|.\|)$, i.e a complete normed vector space over $\mathbb R$, with norm $\|.\|$ (or $\|\cdot\|_{\X}$ in case there is a risk of confusion), its topological dual (or dual for short) will be denoted $\Xstar$. This is simply the space of all linear functionals (aka bras, as referred to by physicists) $\langle \xstar|: \mathcal X \rightarrow \mathbb R$. The bracket (aka dual pairing) $\langle \xstar,x\rangle$ denotes the action of the linear form $\xstar$ (or $\langle \xstar|$, to keep the previous bra terminology) on the point $x \in \X$ (also called a ket, and denoted $|x\rangle$, by physicists), i.e $\langle \xstar,x\rangle := \langle \xstar|(x) := \xstar(x) $. The space $\Xstar$ is a Banach space too, with norm given by

\[\|\xstar\|_* := \sup_{x \in \BX}\langle \xstar,x\rangle. \tag{1}\]

Here $\BX := \{x \in \X \mid \|x\| \le 1\}$ is the unit ball of $\X$. For example if $\mathcal X=\C(\Omega)$ is the space of continuous functions on a compact topological space $\Omega$ endowed with the sup-norm of uniform convergence, namely $\|u\| := \sup_{\omega \in \Omega}|u(\omega)|,$ then $\Xstar:=\M(\Omega)$ is simply the space of Radon measures on $\Omega$. This is a consequence of the celebrated Riesz–Markov–Kakutani representation theorem. For $u \in \C(\Omega)$ and $p \in \M(\Omega)$, the bracket $\langle u,p\rangle$ then corresponds to taking the expectation of the function $u$ w.r.t to the measure $p$, i.e $\langle u,p\rangle := \mathbb E_{\omega \sim p}[u(\omega)] := \int_{\Omega} u dp$.

Except otherwise stated, every Banach space $\X$ considered here will be assumed to be reflexive, which (roughly) means that $\X$ is equal to its respective bi-dual $\Xss$ (the dual of the dual of $\X$).

A bounded linear operator is a linear mapping $A:\X \rightarrow \Y$ between Banach spaces $\X$ and $\Y$ such that the spectral norm $\|A\| := \sup_{x \in \BX} \|Ax\|_{\mathcal Y}$ is finite. The adjoint of $A$ is the linear operator $\Astar:\Ystar \rightarrow \Xstar$, defined implicitly by the duality relation

\[\langle \ystar,Ax\rangle = \langle \Astar\ystar,x\rangle,\;\forall (x,\ystar) \in \X \times \Ystar. \tag{2}\]

For example, if $\X$ and $\Y$ are finite-dimensional real euclidean spaces (think of $\mathbb R^n$ and $\mathbb R^m$), then $A$ is simply a matrix, and $\Astar$ is its transpose!

II.1.3 – Cones, indicator functions, convexity

Given a subset $C \subseteq \X$, we define its indicator function $\chi_C: \mathcal X \rightarrow (-\infty, +\infty]$ by

\[\chi_C(x) = \begin{cases} 0,&\mbox{ if }x \in C,\\ +\infty,&\mbox{ else,} \end{cases} \tag{3}\]

and its support function $\sigma_C:\Xstar \rightarrow (-\infty, +\infty]$ by

\[\sigma_C(\xstar) := \sup_{x \in C}\;\langle \xstar,x\rangle. \tag{4}\]

For example, the dual norm (defined in equation (1)) of the norm on $\X$ is the support function of the unit ball in $\X$.

$C$ is called a cone if it contains all positive rays, i.e if $\lambda C \subseteq C$ for all $\lambda \ge 0$.

The normal cone of $C$ at a point $x \in \X$, denote $N_C(x)$ is defined by

\[N_C(x) := \begin{cases} \{\xstar \in \Xstar \mid \langle \xstar,x'-x\rangle \le 0,\;\forall x' \in C\},&\mbox{ if }x \in C,\\ \emptyset,&\mbox{ else.} \end{cases}\]

The dual cone of $C$ is the subset of $C^\star$ of linear forms on $\X$ which are nonnegative on $C$, i.e

\[C^\star := \{\xstar \in \Xstar \mid \langle \xstar,x\rangle \ge 0,\;\forall x \in C\}.\]

Finally, the polar cone of $C$ is the subset $C^+$ of linear forms on $\X$ which are nonpositive on $C$, i.e

\[C^\circ := \{\xstar \in \Xstar \mid \langle \xstar,x\rangle \le 0,\;\forall x \in C\}.\]

The following observations are immediate:

$C^\circ = -C^\star$
$N_C(x)$, $C^\star$, and $C^\circ$ are convex cones of $\Xstar$.

Recall that a subset $K$ of $\X$ is called convex if the coord connecting every two of its points is a subset of $K$, i.e if $\lambda x + (1-\lambda)x’ \in K$ whenever $x,x’ \in K$ and $\lambda \in [0, 1]$. The convex-hull of any subset $C$ of $\X$ is the smallest subset of $\X$ containing $C$, i.e

\[\conv(C) := \underset{C \subseteq K \subseteq \X,\;K\text{ convex}}{\cap}K.\]

Lemma 2.1.1. For every subset $C$ of $\X$, it holds that

\[\conv(C)=\left\{\sum_{i=1}^nt_i x_i \mid t \in \Delta_n,\;x_1,\ldots,x_n \in C\right\}.\]

Proof. Exercise. Hint: Define $K := \left\{\sum_{i=1}^nt_i x_i \mid t \in \Delta_n,\;x_1,\ldots,x_n \in C\right\}$ and show that

$C \subseteq K$.
$K$ is convex.
If $C \subseteq K’ \subseteq \X$ and $K’$ is convex, then $K \subseteq K’$. Conclude. $\qed$

Given a function $g: \X \rightarrow (-\infty, +\infty]$, it’s effective domain denoted $\dom(g)$ is the subset of $\X$ on which $g$ takes finite values, i.e $\dom(g) := \{x \in \X \mid g(x) < +\infty\}.$ $g$ is said to be proper if it is not equal to infinity everywhere, i.e if there exists $x_0 \in \X$ s.t. $g(x_0) < +\infty$. The epigraph of $g$, denoted $\epi(g)$, is defined by

\[\epi(g) := \{(x, t) \in \X \times \mathbb R \mid g(x) \le t\}.\]

$g$ is said to be a convex function if its $\epi(g)$ is a convex subset of $\X \times \mathbb R$; it is said to be a closed function if $\epi(g)$ is a closed subset of $\X \times \mathbb R$.

II.2 Subdifferentials and the Danskin-Bertsekas Theorem

In the remainder of this exposition, except otherwise stated, $\X$ and $\Y$ will be (reflexive) real Banach spaces.

The subdifferential of $g$ at a point $x \in \X$, denoted $\partial g(x)$, is the subset of $\X$ defined by

\[\partial g(x) := \{v \in \Xstar \mid g(x') \ge g(x) + \langle v,x'-x\rangle\;\forall x' \in \X\} \tag{5}\]

Every $v \in \partial g(x)$ is called a subgradient of $g$ at $x$. Of course, if $g$ is convex and differentiable at $x$, then $\partial g(x) = \{ \nabla f(x) \}$. On the other hand, if $g$ is say the L1 norm on $\mathbb R^n$, then $\partial g(x) = \Pi_{i=1}^n S_i$, where

\[S_i := \partial |\cdot|(x_i) = \begin{cases} \{-1\}, &\mbox{ if }x_i < 0,\\ [-1,1],&\mbox{ if } x_i = 0,\\ \{1\}, &\mbox{ if }x_i > 0. \end{cases}\]

Let $\opt(g)$ be the set of minimizers of the function $g: \X \rightarrow (-\infty,+\infty]$, that is

\[\opt(g) := \{x \in \X \mid g(x') \ge g(x) \; \forall x' \in \X\}.\]

We have the following charaterization, which is reminiscent of the rule “set the derivative to zero!”

Lemma 2.2.1 (Fermat’s Rule). If $g:\X \rightarrow (-\infty, +\infty]$ is a function, then

\[x \in \opt(g) \iff 0 \in \partial g(x).\]

Proof. By direct computation, we get

\[x \in \opt(g) \iff g(x') \ge g(x)\; \forall x' \in \X \iff g(x') \ge g(x) + \langle 0,x'-x\rangle\; \forall x' \in \X \iff 0 \in \partial g(x).\;\qed\]

Lemma 2.2.2 (super-additivity of subdifferential operator). If $g_1,g_2:\X \rightarrow (-\infty, +\infty]$ are functions, then for $x \in \X$, it holds that

\[\partial (g_1 + g_2)(x) \supseteq \partial g_1(x) + \partial g_2(x),\]

where $\partial g_1(x) + \partial g_2(x) :=\{v_1 + v_2 \mid (v_1,v_2) \in \partial g_1(x) \times \partial g_2(x)\}$ is the Minkowski sum of the sets $\partial g_1(x)$ and $\partial g_2(x)$.

Proof. Let $x \in \X$ and $v \in \partial g_1(x) + \partial g_2(x)$. Then there exists $(v_1,v_2) \in \partial g_1(x) \times \partial g_2(x)$ such that $v=v_1+v_2$. Thus for every $x’ \in \X$, by the definition of subdifferentials, we have

\[\begin{split} g_1(x') &\ge g_1(x) + \langle v_1,x'-x\rangle\\ g_2(x') &\ge g_2(x) + \langle v_2,x'-x\rangle.\\ \end{split}\]

Adding both inequalities yields: $(g_1 + g_2)(x’) \ge (g_1 + g_2)(x) + \langle v_1 + v_2,x’-x\rangle$, and so $v_1 + v_2 \in \partial (g_1 + g_2)(x)$. $\qed$

The converse of the set inclusion is not true in general. However, under further conditions, it is.

Lemma 2.2.3 (distributivity of subdifferential). Let $g_1,g_2:\X \rightarrow (-\infty, +\infty]$ be convex functions. If $x \in \dom(g_1) \cap \dom(g_2)$ such that both $g_1$ and $g_2$ are continuous at $x$, then have the identity

\[\partial g_1(x) + \partial g_2(x) = \partial (g_1 + g_2)(x).\]

Proof. Exercise.

Lemma 2.2.4 (subdifferential of composition). Let $A:\X \rightarrow \Y$ be a bounded linear operator and $f:\Y \rightarrow (-\infty, +\infty]$ be a function. Let $g := f \circ A: \X \rightarrow (-\infty, +\infty]$. Then for every $x \in \X$, we have the inclusion

\[\partial g(x) \supseteq \Astar\partial f(Ax) := \{\Astar u \mid u \in \partial f(Ax)\}.\]

Moreover, if there is a point in range of $A$ at which $f$ is finite and, then

\[\partial g(x) = \Astar \partial f(Ax) := \{\Astar v \mid v \in \partial f(Ax)\}.\]

Proof. Let $v \in \Astar\partial f(Ax)$. Then $\exists u \in \partial f(Ax) \st v = \Astar u$. Now, for any $x’ \in \X$, one has

\[\begin{split} g(x') := f(Ax') \ge f(Ax) + \langle u,Ax'-Ax\rangle = f(Ax) + \langle \Astar u,x'-x\rangle = f(Ax) + \langle v,x'-x\rangle, \end{split}\]

where the first inequality is because $u \in \partial f(Ax)$, the second equality is by properieties (see formula (1)) of the dual pairing $\langle \cdot,\cdot\rangle: \Xstar \times \X \rightarrow \mathbb R$, and the last equality is because $v=\Astar u$. Thus we get that $v \in \partial g$, and so $\partial g(x) \supseteq \Astar \partial f(Ax)$ as claimed.

The second part of the lemma is not that easy to prove…

Lemma 2.2.5 (subdifferential of indicator funciton). Let $C$ be a subset of $\X$. Then the subdifferential of the indicator function $\chi_C$ at the point $x \in \X$ is the normal cone $N_C(x)$.

Proof. Direct computation.

We are now en route for more fun stuff.

II.3 – Danskin-Bertsekas Theorem for subdifferentials

The Danskin Theorem is a very important result in optimization which allows us to differentiate through an optimization problem. It was extended by Bertsekas (in his PhD thesis!) to subdifferentials, thereby opening the door to connections with convex optimization. To motivate the need for such a result, consider the following non-tricky problems.

What is the subdifferential on the $\ell_\infty$-norm on $\mathbb R^m$ ?
What is the subdifferential of the function $h: \mathbb R^2 \rightarrow (-\infty, +\infty]$, defined by $h(x_1,x_2) = \max(2019, 2x_1 - 3, x^2)$ ?

The reader who tries workout the above questions manually will be very seriously unhappy with the experience.

Theorem 2.3.2 (Danskin-Bertsekas Theorem for subdifferentials). Let $\Phi: \mathbb R^n \times \Y \rightarrow (-\infty, +\infty]$ be a function and $C$ be a nonempty compact subset of $\mathbb R^n$. Assume further that for every $x \in C$, the mapping $\Phi(x, \cdot) : \Y \rightarrow (-\infty, +\infty]$ is a closed proper convex function. Consider the function $f: \Y \rightarrow (-\infty, +\infty]$ defined by $f(y) := \underset{x \in C}{\text{sup }}\Phi(x, y).$ If $f$ is proper, then it is closed and convex. Furthermore, if $\inte(\dom(f)) \ne \emptyset$ and $\Phi$ is continuous on $\mathbb R^n \times \inte(\dom(f))$, then for every $y \in \inte(\dom(f))$ we have

\[\partial f(y) = \text{conv}\{\partial_y \Phi(x, y) \mid x \in C_y\},\]

where $C_y := C \cap \opt(\Phi(\cdot,y)) := \{x \in C \mid \Phi(x, y) = f(y)\}$.

Proof. Classical result.

Using the above theorem, one can easily establish the following lemma.

Lemma 2.3.3 (subdifferential of pointwise max of $n$ functions). Let $f_1,\ldots,f_n: \Y \rightarrow (-\infty, +\infty]$ be convex functions. Then for every $y \in \cap_{i=1}^n\dom(f_i)$ such that each $f_i$ is continuous at $y$, one has the identity

\[\partial \max(f_1,\ldots,f_n)(y) = \conv(\cup_{i=1}^n \partial f_i(y)).\]

Proof. Let $f := \max(f_1,\ldots,f_n)$. Define $\Phi:\mathbb R^n \times \Y \rightarrow (-\infty, +\infty]$ by $\Phi(x,y):=\sum_{i=1}^n x_i f_i(y)$ and note that $f(y) = \sup_{x \in \Delta_n}\Phi(x, y)$ for every $y \in \Y$. Also note that $\partial_y \Phi(x, y) = \sum_{i=1}^nx_i\partial f(y)$. Now invoke Theorem 2.2.2 and conclude. $\qed$

Exercise 2.3.1. Show that the subdifferential of the norm $\|\cdot\|$ on a Banach space $\X$ is given by

\[\partial \|\cdot\|(x) = \{\xstar \in \BXstar \mid \langle \xstar,x\rangle = \|x\|\}.\]

Hint. Noting that $\|.\|$ is the support function of the unit ball in the dual space $\Xstar$, invoke Theorem 2.3.2.

II.4 – Fenchel conjugates, the “Fourier transform” of convex analysis!

In Harmonic analysis, the Fourier transform of the convolution of functions is the product of their Fourier transforms. This property of the Fourier transform comes in handy as it allows one to solve problems in Harmonic analysis, by first mapping them in the Fourier domain in which things might be considerably simpler. In convex analysis, the Fenchel conjugate of the “infimal convolution” of functions is the sum of their Fenchel conjugates!

The Fenchel conjugate (aka Fenchel-Legendre transform, aka convex conjugate) of a function $g:\X \rightarrow (-\infty, +\infty]$ is the function $\gstar:\Xstar \rightarrow (-\infty, +\infty]$ defined by

\[\gstar(\xstar) := \sup_{x \in \X}\;\langle \xstar,x\rangle - g(x). \tag{6}\]

Because $\gstar$ is a point-wise supremum of affine functions, it is automatically convex, even when $g$ is not convex! The bi-conjugate of $g$, denoted $\gss:\Xss (= \X) \rightarrow \Yss (= \Y)$, is defined as the Fenchel conjugate of $g^*$ (i.e the Fenchel conjugate of the Fenchel conjugate).

The following is a generalization of the well-known Hoelder’s inequality.

Lemma 2.4.1 (Fenchel-Young inequality). $g(x) + \gstar(\xstar) \ge \langle \xstar,x\rangle$ for all $(x,\xstar) \in \X \times \Xstar$. Moreover, for all $(x,\xstar) \in \dom(g) \times \Xstar$, the following statements are equivalent:

(a) $g(x) + \gstar(\xstar) = \langle \xstar,x\rangle$.
(b) $\xstar \in \partial g(x)$.

Proof. The first part follows directly from the definition of $\gstar(\xstar)$ as the supremum over $x$ of $\langle \xstar,x\rangle - g(x)$. Under the assumption that $(x,\xstar) \in \dom(g) \times \Xstar$, we have

\[\begin{split} \xstar \in \partial g(x) &\iff g(x') \ge g(x) + \langle \xstar,x' - x\rangle\;\forall x' \in \X\\ &\iff \langle \xstar,x \rangle - g(x) \ge \langle \xstar,x'\rangle - g(x')\;\forall x' \in \X\\ &\iff \langle \xstar,x\rangle - g(x) = \gstar(\xstar),\text{ i.e }\;g(x) + \gstar(\xstar) = \langle \xstar,x\rangle.\;\qed \end{split}\]

Using the above Lemma, it’s not hard to show (Exercise 2.6.6) that $g \ge \gss$.

Lemma 2.4.2 (Fenchel conjugate of indicator function). Let $C$ be a subset of $\X$. Then the Fenchel conjugate of the indicator function $\chi_C$ is the support function of $C$, that is $\chi_C^\star = \sigma_C$.

Moreover, if $C$ is a cone, then $\chi_C^\star = \chi_{C^\circ}$, the indicator function of the polar cone of $C$.

Proof. Indeed, for every $\xstar \in \X$, one has

\[\chi_C(\xstar) := \sup_{x \in \X}\;\langle \xstar,x\rangle - \chi_C(x) = \sup_{x \in C}\;\langle \xstar,x\rangle =: \sigma_C(\xstar).\]

Now, suppose $C$ is a cone. If $\xstar \in C^+$, then $\langle \xstar,x\rangle \le 0$ for all $x \in C$ and this lower bound is attained, since $0 \in C$ as $C$ is a cone. Thus $\chi_C(\xstar) = \sup_{x \in C}\;\langle \xstar,x\rangle = 0$. One the other hand, if $\xstar \not \in C^\circ$, then there exists $x_0 \in C$ such that $\langle \xstar,x_0\rangle > 0$. Since the nonnegative ray $R^+(x_0) := \{\lambda x_0 \mid \lambda \ge 0\}$ is contained in $C$ (as the latter is a cone), it follows that

\[\chi_C(\xstar) = \sup_{x \in C}\;\langle \xstar,x\rangle \ge \sup_{x \in R^+(x_0)}\;\langle \xstar,x\rangle = \sup_{\lambda \ge 0}\lambda \langle \xstar,x_0\rangle = +\infty, \text{ because } \langle \xstar,x_0\rangle > 0.\]

Therefore $\chi_C^\star = \chi_{C^\circ}$ as claimed. $\qed$

II.4.1 – Infimal convolutions and decomposition theorem

Given functions $g_1,\ldots,g_k:\X \rightarrow (-\infty, +\infty]$, their infimal convolution is the function $\Box_{i=1}^k g_i :\X \rightarrow (-\infty, +\infty]$ defined by

\[(\Box_{i=1}^k g_i)(x) := \inf_{x_1,\ldots x_k \in \X}\sum_{i=1}^k g_i(x_i) \st \sum_{i=1}^k x_i = x.\]

Theorem 2.4.2 (Fenchel conjugate of inf-convolution). Let $g_1,\ldots,g_k:\X \rightarrow (-\infty, +\infty]$. Then

\[(\Box_{i=1}^k g_i)^\star = \sum_{i=1}^k \gstar_i.\]

Proof. Let $ g:=\Box_{i=1}^k g_i$. For every $\xstar \in \Xstar$, one computes

\[\begin{split} g^*(\xstar) &:= \sup_{x}\; \langle \xstar,x\rangle - g(x) \overset{(a)}{=} \sup_{x}\;\langle \xstar,x\rangle - \inf_{x_1,\ldots,x_k \in \X}\left\{\sum_i g_i(x_i) \mid \sum_i x_i = x\right\}\\ &\overset{(b)}{=} \sup_{x}\;\langle \xstar,x\rangle + \sup_{x_1,\ldots,x_k}\left\{-\sum_i g_i(x_i) \mid \sum_i x_i = x\right\}\\ & \overset{(c)}{=} \sup_{x,x_1,\ldots,x_k}\left\{\langle \xstar,x\rangle -\sum_i g_i(x_i) \mid \sum_i x_i = y\right\} \\ &\overset{(d)}{=} \sup_{x,x_1,\ldots,x_k}\langle \xstar,\sum_i x_i\rangle -\sum_i g_i(x_i) \overset{(e)}{=} \sup_{y,x_1,\ldots,x_k}\sum_i \langle \xstar,x_i\rangle -g_i(x_i)\\ &\overset{(f)}{=} \sum_i\sup_{x_i}\;\langle\xstar,x\rangle - g_i(x_i) \overset{(*)}{=} \sum_i g_i^*(x), \end{split}\]

where

(a) is just plugging-in the definition of $g(x)$.
(b) is because $-\inf something = -\sup-thatthing$ .
(c) is an application of Exercise 1.2.2.
(d) is just substituting the constraint $x=\sum_i x_i$ to get $\langle \xstar,x\rangle = \langle \xstar,\sum_i x_i\rangle$. After this substitution, the variable $x$ doesn’t play a role anymore in the maximization, and so can be deleted.
(e) is because $\langle \xstar,\sum_i x_i\rangle - \sum_i g_i(x_i) = \sum_i \langle \xstar,x_i\rangle - \sum_i g_i(x_i)=\sum_i\langle \xstar,x_i\rangle - g_i(x_i)$.
(f) is an application of Exercise 1.2.2.
(*) is because $g_i^*(x) := \sup_{x_i \in \X}\langle \xstar,x_i\rangle - g_i(x_i)$ by definition. $\qed$

Lemma 2.4.4 (Convexity of inf-convolution of convex functions). If $g_1,\ldots,g_k:\X \rightarrow (-\infty, +\infty]$ are convex, then so is their inf-convolution $\Box_{i=1}^k g_i$.

Proof. See https://math.stackexchange.com/a/1598296/168758.

Exercise 2.4.2. Show that he Fenchel conjugate of the (multivariate) Huber function $h:\mathbb R^n \rightarrow \mathbb R$, defined by

\[h(x) := \begin{cases} (1/2)\|x\|_2^2,&\mbox{ if }\|x\|_1 \le 1,\\ \|x\|_1 - 1/2,&\mbox { else} \end{cases}\]

is given by

\[h(\xstar) = \begin{cases} (1/2)\|\xstar\|_2^2,&\mbox{ if }\|\xstar\|_\infty \le 1,\\ +\infty,&\mbox{ else.} \end{cases}\]

Hint. Show that $h = \|\cdot\|_1 + (1/2)\|\cdot\|_2^2$ and then invoke Theorem 2.4.2.

II.5 – Some worked examples

Example 2.5.1 (Fenchel transform of norms). Let $\X$ be a (reflexive) Banach space with dual $\Xstar$. Using the fact that $\|x\| \equiv \underset{z \in \Xstar,\;\|z\|_* \le 1}{\sup }\langle z,x\rangle$, we immediately get

\[\begin{split} \underset{x \in \X}{\text{sup }}\langle \xstar,x\rangle - \|x\| &= \underset{x \in \X}{\sup}\;\langle \xstar,x\rangle - \underset{z \in \Xstar,\;\|z\|_* \le 1}{\sup }\langle z,x\rangle = \underset{z \in \Xstar,\; \|z\|_* \le 1}{\inf }\underset{x \in \X}{\sup}\;\langle \xstar-z,x\rangle \\ &= \underset{z \in \Xstar,\; \|z\|_* \le 1}{\inf } \begin{cases} 0,&\mbox { if }z = \xstar,\\ +\infty, &\mbox{ otherwise} \end{cases}\\ &= \begin{cases}0,&\mbox { if }\|\xstar\|_* \le 1,\\+\infty, &\mbox{ otherwise,}\end{cases} \end{split}\]

where the second equality follows from Sion’s minimax theorem (as an easy exercise, the reader should check that the hypotheses of the Theorem are satisfied). Thus $\|.\|^* = \chi_{\BXstar},$ the indicator function of the dual unit ball.

Example 2.5.2 (Fenchel transform of linear functionals). Let $\X$ be a Banach space and $c \in \Xstar$. Consider the function $g:\X \rightarrow (-\infty, +\infty]$ defined by $g(x) := \langle c, x\rangle$. BTW, this function can be identified with a point $\langle c|$ of $\Xstar$. One computes the Fenchel conjugate of $g$ as $\gstar(\xstar) := \sup_{x \in \X}\langle \xstar,x\rangle - g(x) = \sup_{x \in \X}\langle \xstar - c,x\rangle = \chi_{\{c\}}(\xstar) = \begin{cases} 0,&\mbox{ if }\xstar = c,\\ +\infty,&\mbox{ else.} \end{cases}$

II.6 Exercises

Exercise 2.6.1. What is the Fenchel conjugate of the function $g:\mathbb R^n \rightarrow (-\infty, +\infty]$ defined by $g(x) := \max (x_1,\ldots,x_n)$ ?

Exercise 2.6.2. (basic properties of Fenchel conjugates.) Given a function $g:\X \rightarrow (-\infty, +\infty]$ and scalar $\lambda > 0$, $\alpha \in \mathbb R$, and $x_0 \in \X$ prove that:

$(x \mapsto \lambda g(x))^\star(\xstar) \equiv \lambda \gstar(\xstar/\lambda)$
$(x \mapsto g(x + x_0))^\star(x) \equiv \gstar(\xstar) - \langle \xstar, x_0\rangle$.
$(x \mapsto \alpha + g(x))^\star(x) \equiv \gstar(\xstar) - \alpha$.
More generally, let $x_0 \in \X$, $\gamma \in \mathbb R\setminus\{0\}$, $\lambda > 0$, and $c \in \Xstar$, and define the function $h:\X \rightarrow (-\infty, +\infty]$ by $h(x) := \alpha + \langle c,x\rangle + \lambda g(\gamma x + x_0)$. Prove that

\[h^\star(\xstar) = \lambda \gstar((\lambda\gamma)^{-1}(\xstar - c)) - \gamma^{-1}\langle \xstar - c,x_0\rangle - \alpha.\]

Hint. Notice that all the other sub-problems in this exercise are special instances of the last. To solve the last sub-problem (and therefore solve all the others by the same token), use the invertible change of variable $x := \gamma^{-1}(\tilde{x} - x_0)$ to get

\[\begin{split} \langle \xstar,x\rangle - h(x) &= -\alpha + \langle \xstar - c,x\rangle - \lambda g(\gamma x + x_0)\\ &= \lambda(-\gamma^{-1} \langle (\lambda\gamma)^{-1}(\xstar-c),\tilde{x}\rangle - g(\tilde{x})) - \gamma^{-1}\langle \xstar-c,x_0\rangle -\alpha. \end{split}\]

Now optimize over $\tilde{x} \in \X$ and use the definition of $\gstar$ to get the claimed formula.

Exercise 2.6.4. Let $\Omega$ be a compact probability space (e.g a probability simplex) and $p$ be a distribution thereupon. Show that negative-entropy $\M(\Omega) \mapsto (-\infty,+\infty]$ defined by

\[H_{p}(q) := \kl(q\|p) :=\mathbb E_{\omega \sim q}\left[\log(q(\omega)/p(\omega))\right]\]

and $\softmax_{p}: \C(\Omega) \rightarrow (-\infty,+\infty]$ defined by

\[\softmax_{p}(u) := \log\mathbb E_{x \sim p}[\exp(u(x))]\]

are Fenchel conjugates of each another.

Hint. Direct computation.

Exercise 2.6.5 (entropy). Let $a \in \mathbb R^n$ and $\sigma_1,\ldots,\sigma_n > 0$, and consider the function $g:\mathbb R^n \rightarrow (-\infty, +\infty]$ defined by $g(x)= \begin{cases} \|x\|_1,&\mbox { if }\sum_{i=1}^n \sigma_i^2x_i^2 \le 1,\\ +\infty,&\mbox{ else.} \end{cases}$

Show that

\[\gstar(\xstar) = \sum_{i=1}^n\sigma_i^{-2}\max(|\xstar|-1, 0)^2_,\;\forall \xstar \in \mathbb R^n.\]

\[\gstar(\xstar) = \underset{z \in \mathbb R^n,\;\|z\|_\infty \le 1}{\min}\;\sqrt{\sum_{i=1}^n(z_i-\xstar_i)^2},\]

a simple separable optimization problem which can be solved implicitly to get eh claimed expression.

Exercise 2.6.6. Given a function $g:\X \rightarrow (-\infty, +\infty]$, show that $g(x) \ge \gss(x)$ for all $x \in \X$.

Hint. Use Lemma 2.4.1 (Fenchel-Young inequality).

III – The Fenchel-Rockafellar duality theorem

III.1 Motivating Example: Conic Programming (CP)

We motivate things with Conic Programming (CP), a generalization of Linear Programming (LP), a sub-field of convex optimization which basically gave birth to convex optimization and convex convex analysis (thanks to Lionid Kantorovich, R.T Rockafellar, Jean-Jaques Moreau, etc.). So, consider the case where $\Y$ be a real Banach space, and $\X$ and $A$ be as before. Let $b \in \Y$, $c \in \Xstar$, and $C$ be a cone of $\Y$. Consider the problem

\[p = \inf_{Ax - b \in C}\langle c, x\rangle \tag{CP}.\]

Of course, the case $C := \{y \in \Y \mid y \ge 0\}$ corresponds to linear programming. Now, it’s well-know that the “dual” of the above problem is the problem

\[d=\sup_{\ystar \in \Ystar,\; \ystar \in C^\star,\;\Astar\ystar = c}\langle \ystar, b\rangle, \tag{Dual-CP}\]

where $C^\star := \{\ystar \in \Ystar \mid \langle \ystar,y\rangle \ge 0,\;\forall y \in C\}$ is the dual cone of $C$. Moreover, one has $p \ge d$ with equality under certain delicate conditions.

But where the heck does this correspondence come from ?

In a sense, the aim of this blogpost to explain this correspondence, using the modern framework of convex analysis. I mean “modern” in the sense that we won’t be talking about things like “slack variables”, “slater’s condition”, “Lagrange multipliers”, etc. Only Fenchel conjugates, subdifferentials, etc. We will still be talking about Karush-Kuhn-Tucker (KKT) conditions though.

Now, one first observes that problem (CP) above can be succinctly rewritten as

\[p=\inf_{x \in \X}f(Ax) + g(x) \tag{P}\]

by defining $g:\X \rightarrow (-\infty, +\infty]$ by $g(x) := \langle c, x\rangle$, and $f:\Y \rightarrow (-\infty,+\infty]$ by

\[f(y) := \begin{cases} 0,&\mbox{ if }y - b \in C,\\ +\infty,&\mbox{ else.} \end{cases}\]

III.2 Towards the FRDT

In general, let $\X$ and $\Y$ be (reflexive) Banach spaces and $A:\X \rightarrow \Y$ be a bounded linear operator. Let $g:\X \rightarrow (-\infty, +\infty]$ and $f: \Y \rightarrow (-\infty, +\infty]$ be functions (not necessarily convex!), and consider the optimization (P). From (7), it holds that $f(Ax) \ge \fss(Ax)$ (Exericise 2.6.6), and so one computes

\[\begin{split} p := \inf_{x \in \X}\; f(Ax) + g(x) &\ge \inf_{x \in \X}\; \sup_{\ystar \in \Ystar} \langle \xstar,Ax\rangle - \fstar(\ystar) + g(x)\\ & \overset{(a)}{\ge} \sup_{\ystar \in \Ystar}\inf_{x \in \X} \;\langle \ystar,Ax\rangle - \fstar(\ystar) + g(x)\\ & = \sup_{\ystar \in \Ystar}-\fstar(\ystar) + \inf_{x \in \X} \;\langle \Astar\ystar,x\rangle - g(x)\\ & \overset{(b)}{=} \sup_{\ystar \in \Ystar}-\fstar(\ystar) - \sup_{x \in \X} \;\langle -\Astar\ystar,x\rangle - g(x)\\ & \overset{(c)}{=} \sup_{\ystar \in \Ystar}-\fstar(\ystar) - \gstar(-\Astar\ystar). \end{split}\]

where

(a) follows from Exercise 1.2.1.
(b) is (2) and the fact that $\inf stuff = -\sup(-stuff)$.
(c) is by definition of $\gstar$ (see (6)).

Thus, if we define define the function $\Phi:\X \times \Ystar \rightarrow (-\infty, +\infty]$ by $\Phi(x,\ystar) := \langle \ystar,Ax\rangle - \fstar(\ystar) + g(x)$, and consider the dual problem

\[d = \sup_{\ystar \in \Ystar}\; -\fstar(-\ystar) - \gstar(\Astar\ystar), \tag{D}\]

and the primal-dual problem

\[\underline{p} = \sup_{\ystar \in \Ystar}\inf_{x \in \X} \;\Phi(x,\ystar), \tag{PD}\]

and finally the dual-primal problem

\[\overline{d} = \inf_{x \in \X}\sup_{\ystar \in \Ystar} \;\Phi(x,\ystar), \tag{DP}\]

one has the chain of inequalities

\[p \ge \underline{p} \ge \overline{d} \ge d.\]

The difference $p - d$ (only defined when $d < \infty$ is called the duality gap, and we say there is strong duality in case this gap equals $0$, i.e $p=d$.

Back to conic programming. Returning to conic programming (the problem (CP) above), we already showed in section III.1 that the Fenchel congugate of the linear function $g:\X \rightarrow (-\infty,+\infty]$ defined by $g(x) := \langle c,x\rangle$ is $\gstar(\xstar) = \chi_{\{c\}}(\xstar), \;\forall \xstar \in \Xstar$ the indicator function of the singleton $\{c\} \subseteq \Xstar$. It remains to compute the Fenchel conjugate of the function $f:\Y \rightarrow (-\infty, +\infty]$ defined by

\[f(y) := \begin{cases} 0,&\mbox{ if }y - b \in C,\\ +\infty,&\mbox{ else.} \end{cases}\]

Now, by direct computation, we have

\[\begin{split} \fstar(\ystar) := \sup_{y \in \Ystar}\; \langle \ystar, y\rangle - f(y) = \sup_{y - b \in C}\;\langle \ystar,y\rangle &= \langle \ystar,b\rangle + \sup_{y \in C}\;\langle \ystar,y\rangle\\ &= \begin{cases} \langle \ystar, b\rangle,&\mbox{ if }\ystar \in C^\circ=-C^\star\\ +\infty,&\mbox{ else,} \end{cases} \end{split}\]

where the last equality is an application of Lemma 2.4.2. Thus in view of the general dual problem (D) above, we have

\[d_{LP} = \sup_{\ystar \in \Ystar} -\fstar(-\ystar) - \gstar(\Astar\ystar) = \sup_{\ystar \in \Ystar,\; \ystar \in C^\star,\;\Astar\ystar = c}\langle \ystar,b\rangle,\]

which is the dual conic program (Dual-CP).

Next time. The FRDT prescribes sufficient conditions under which there is strong duality. Thus far, we haven’t talked much about convexity; we didn’t have to! It’s been about functional analysis (linear algebra, to be honest). In subsequent posts, we will see more convexity and dive into the FRDT proper. We won’t go very far without the celebrated Hann-Banach seperation theorem.

To be continued…