Cohomology is a central concept in algebraic topology and geometry. Oddly enough, this theory applies to certain concrete problems arising in machine learning (e.g globally consistent ranking of items in an online shop like Amazon or NetFlix) and game theory (e.g approximating multi-player non-cooperative games with potential games, in view of computing approximate Nash equilibria of the former).

This is the first of a unified series of posts to explore the main ideas behind these developments. We will start by a short promenade which ends up with the so-called Hodge-decomposition, the central tool. Then In the subsequent posts we shall

  • construct the de Rham cohomology and Hodge decomposition of an abstract simplicial complex

  • apply these constructions to ranking –obtaining the so-called HodgeRank– and to game theory

  • write some python code!

Initial motivation

My interest in these things got sparkled after a very productive discussion with Anna Korba on a problem I was trying to solve: how to approximate a digraph (directed graph) with a DAG (directed acyclic graph), without “losing too much information”’. It turns out that this problem is completely solved by the Hodge decomposition on the space of flows on the edges, and then keeping only the curl-free component, which in fact is a DAG (no cycles)!

Prerequisites

The ideas presented here should be directly accessible to anyone bearing even just a skimpy acquaintance with the following elementary concepts (in decreasing order of importance)

  • Algebra: sets, Abelian groups, vector spaces matrices / linear transformations, kernel, image, dual space, rank-nullity theorem

  • Differential geometry: the idea of a smooth manifold, scalar and vector fields, differential forms, gradient, divergence, curl, Stokes theorem

That notwithstanding, as we go along I shall try my best to review some of these concepts in context, to the minimal amount of detail which is sufficient for my purposes.

\[\def\im{\operatorname{im}} \def\grad{\operatorname{grad}} \def\curl{\operatorname{curl}} \def\div{\operatorname{div}} \def\dim{\operatorname{dim}}\]

A criminal’s view on cohomology

It is well known that on an $n$-dimensional smooth manifold $M$ (Def: $M$ is a topological space in which each point $x \in M$ has a neighborhood $U_x \ni x$ which is homeomorphic to an open subset $V_x$ of $\mathbb R^n$), a conservative vector field is irrotational, i.e

\[\text{curl}(\underbrace{\text{grad}(f)}_{\text{conservative}}) = 0,\]

for any smooth function $f: M \rightarrow \mathbb R$. Recall that a smooth function on $M$ is one which is infinitely differentiable on $M$, and we’ll say that $f$ is of class $\mathcal C^\infty$ on $M$ or simply write $f \in \mathcal C^\infty(M)$. Also recall that $\operatorname{grad}(f) := \left(\frac{\partial f}{\partial x_1},\ldots,\frac{\partial f}{\partial x_n}\right) = \sum_{i}\frac{\partial f}{\partial x_i} dx_i$, a differential $1$-form on $M$. As regards the object “$dx_i$”, it should be seen as a linear form on the tangent bundle, which returns the $i$th component of a (co-)vector, i.e $dx_i(a) = a_i$.

Question (Q1): Is the converse true ? That is if $X$ is a vector field with $\text{curl}(X) = 0$, is it true that $X = \grad(f)$, the gradient of some scalar potential field $f$ ?

Example of “global obstruction” to (Q1)

Let’s produce an examplar scenario where (Q1) has a non-affirmative answer. Let $M = \mathbb R - \{(0,0)\}$, i.e the plane with the origin removed, and consider the vector field defined on $M$ by $X(x, y) := \left(-\frac{y}{x^2 + y^2}, \frac{x}{x^2 + y^2}\right)$. By Stoke’s Theorem, it is clear that the flux of $X$ along every closed loop which goes clockwise around the origin once is non-zero. This is because $X(x, y)$ is always a tangent at $(x, y)$, and points clockwise. However, a direct computation shows that $\text{curl}(X) = 0$.

Cohomological reformulation of (Q1)

In question (Q1), ultimately, the interesting problem is the estimation of the size of the group

\[H^1 := \dfrac{\text{ker}(\text{curl})}{\text{im}(\text{grad})} := \{X + \text{im}(\text{grad})\;|\;X\text{ is a vector field with }\curl(X) = 0\},\]

where $ X + \im(\grad) := \{ X + \grad(f)\;|\; f \text{ is a smooth function on }M \}, $ all the vector fields which are equal to $X$, up to within an irrational error. If $|H^1| = 1$ so that $H^1(M, \mathbb R) = \{ 0 \}$ and $\text{ker}(\text{curl}) = \text{im}(\text{grad})$, then the answer to the above question (Q1) is affirmative. Thus $H^1$ measures the “obstruction” to answering (Q1) affirmatively. The “$H$” in $H^1$ denotes the homology in co-homology, a concept which we will now explore.

The de Rham co-chain complexe of $M$ is the chain

\[0 \longrightarrow \Omega^0(M) \overset{d^1=\operatorname{grad}}{\longrightarrow} \Omega^1(M) \overset{d^2=\operatorname{curl}}{\longrightarrow} \Omega^2(M) \overset{d^3}{\longrightarrow} \ldots \Omega^{k-1}(M) \overset{d^k}{\longrightarrow} \Omega^{k}(M) \ldots \overset{d^n}{\longrightarrow} \Omega^n(M) \longrightarrow 0.\]

Here, $\Omega^k(M)$ denotes the vector space of all differential $k$-forms on $M$. It is the span of $k$-fold wedge products of the form $dx_{i_1} \wedge \ldots \wedge dx_{i_k}$ whose coefficients are smooth functions on $M$. $\Omega^0(M)$ is simply this ring denoted $\mathcal C^\infty(M)$, of $\mathcal C^\infty$ real-valued functions on $M$. For $k \ne 0$, $\Omega^k(M)$ has the structure of a $\mathcal C^\infty(M)$-module. It’s not hard to see that $\Omega^k(M)$ has (algebraic) rank ${n\choose k}$, since this number precisely counts how many unique ways one can form the products $dx_{i_1} \wedge \ldots \wedge dx_{i_k}$, modulo the ordering of the terms. Also, since ${n\choose n-k} = {n\choose k}$, it follows that $\Omega^k \cong \Omega^{n-k}$ as $\mathcal C^\infty(M)$-modules.

The symbol $d^k$ is the restriction on $\Omega^k(M)$ of the exterior derivative $d$ of the manifold $M$. All we need to know here is that $d$ is a function defined on the exterior graduated algebra $\Omega(M) := \oplus_k \Omega^k(M)$ and is constrained to uniquely satisfy many properties, the most important being $d \circ d = 0$. This in turn implies that $d^{k+1} \circ d^k = 0$, i.e $\im(d^k)$ is a subspace of $\ker(d^{k+1})$ for all $k$, which is nothing but an exotic higher-order reformulation of the principle we saw in the of this post, namely that every conservative vector field is irrotational!

It should be noted that the wedge product defining the elements of the $\Omega^k(M)$ is anti-symmetric, meaning that if the terms in $dx_{i_1} \wedge \ldots \wedge dx_{i_k}$ are permuted, then the result product picks up a sign equal to the sign of the applied permutation. Thus in particular, $\Omega^1(M)$ is the space of anti-symmetric vector fields on $M$.

One may now form the group

\[H^k(M,\mathbb R) := \dfrac{\operatorname{ker}(d^{k+1})}{\operatorname{im}(d^k)},\]

called the $k$th de Rham cohomology of $M$. Amongst many other fabulous predictions, one can show that if $M$ and $M’$ are of same “homotopy type” (e.g the whole of $\mathbb R^n$ has the same homotopy type as any point in it! Two smooth curves with the same endpoints have the same homotopy type. And so on…), then they have the same cohomology.

In this new parlance, one restate (Q1) as asking whether the 1st De cohomology

\[H^1(M, \mathbb R) := \dfrac{\operatorname{ker}(d^2)}{\operatorname{im}(d^1)} = \dfrac{\operatorname{ker}(\operatorname{curl})}{\operatorname{im}(\operatorname{grad})}\]

of $M$ is trivial. Of course, the answer depends on the global geometry of $M$. Indeed, if $M$ is flat (i.e $M$ is homotopy equivalent to $\mathbb R^n$, denoted $M \simeq \mathbb R^n$), then the answer is affirmative because $\mathbb R^n \simeq \{0\}$, and so has the same cohomology (up to withing group isomorphism). It follows in particular that

\[H^k(M,\mathbb R) \cong H^k(\mathbb R^n,\mathbb R) \cong H^k(\{0\},\mathbb R) \cong \begin{cases} \mathbb R,&\mbox{ if }n > 0,\; k = 0,\\ \{0\},&\mbox{ else.} \end{cases}\]

Since a smooth manifold is locally flat, it then follows that the answer to (Q1) is affirmative, locally, without any restrictions on $M$. This is precisely the Poincaré Lemma: every irrotational vector field is locally conservative!

Some “computations”

To wrap up this introductory section, let’s note the following algebraic topological facts about the de Rham cohomology:

  • (1) $H^0(M, \mathbb R) = \ker(\grad)/\{0\} = \ker(\grad) \cong \mathbb R^c$, where $c$ is the number of “topologically connected components” of $M$.
  • (2) If $M$ is compact and orientable, then $H^n(M, \mathbb R)$ is non-trivial, i.e $\dim H^n(M, \mathbb R) \ge 1$.

The Hodge decomposition

We now see how to “compress” a manifold via linear algebra. If $M$ is Riemannian, so that it has a metric, then for each $k$ we can define a (generalized) divergence operator, $\delta_k: \Omega^k(M) \rightarrow \Omega^{k-1}$ by $\langle \delta_k X, f \rangle_{\Omega^{k-1}(M)} = \langle X, d^k(f)\rangle_{\Omega^k(M)}, $ which is the adjoint of $d^k$. We can then define the generalized Hermoltzian (aka Laplacian) of $M$, namely the elliptic differential operator

\[\Delta_k := d^k \delta_k + \delta_{k+1}d^{k+1} : \Omega^k(M) \rightarrow \Omega^k(M),\]

whose kernel is the space of harmonic functions

\[\mathcal H^k(M,\mathbb R) := \operatorname{ker}(\Delta_k).\]

Theorem (Hodge decomposition).

  • (a) We have the group isomorphism
\[\mathcal H^k(M,\mathbb R) \cong \ker(\delta_k) \cap \ker(d^{k + 1}).\]
  • (b) If $M$ is compact, then $H^k(M,\mathbb R) \cong \mathcal H^k(M,\mathbb R)$, and we have the orthogonal decomposition

\begin{equation} \Omega^k(M) = \im(d^{k-1}) \oplus \mathcal H^k(M,\mathbb R) \oplus \im(\delta_k). \end{equation}

In particular for the case $k = 1$, we have the decomposition

\begin{equation} \Omega^k(M) = \im(\grad) \oplus \mathcal H^1(M,\mathbb R) \oplus \im(\curl). \end{equation}

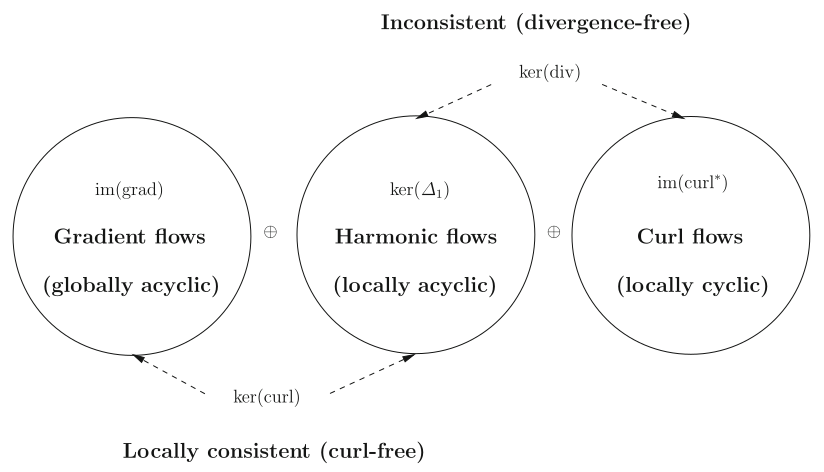(Figure is courtesy of Jiang et al. “Statistical ranking and combinatorial Hodge theory”)

Sketch of proof. Soitent $A$, $B$ des matrices avec $AB = 0$, et donc $\im(A) \subseteq \ker(B)$. Soit la matrice $\Delta := A^* A + BB^* $, matrice psd d’ordre $n$. Il n’est pas difficile de montrer que son noyeau vaut $\ker(\Delta) = \ker(A^* ) \cap \ker(B)$, qui est biensur isomorphe au groupe $H^1 :=\ker(A)/\im(B)$. Par le theoreme de décomposition de Fredholm (algèbre liniaire élementaire) et le fait que $\Delta^* = \Delta$, l’on a

\[\mathbb R^n = \ker(\Delta) \oplus \ker(\Delta)^\perp = \ker(\Delta) \oplus \im(\Delta) = H^1 \oplus \im(A^* ) \oplus \im(B).\]

Il suffit alors the prendre $A = d^{k+1}$ et $B = d^k$ pour obtenir l’annoncé. $\quad\quad\quad\quad\quad\quad\quad\quad\quad\Box$

Next time

In the next post we shall

  • construct the de Rham cohomology and Hodge decomposition of an abstract simplicial complex

  • apply these constructions to ranking –obtaining the so-called HodgeRank– and to game theory

  • write some python code!

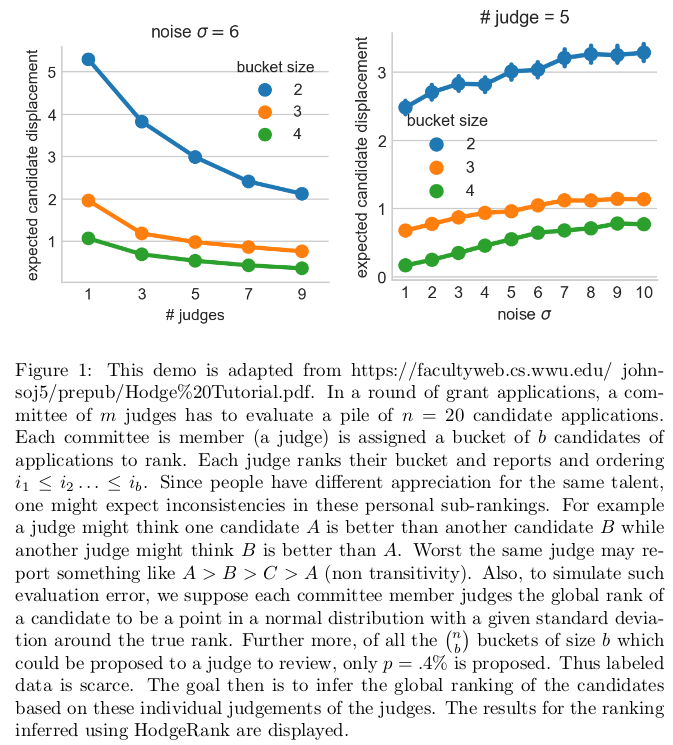
The figure below is a glimpse.