In our OPT2016 NIPS workshop paper, we propose a simple projection-free primal-dual algorithm for computing approxi- mate Nash-equilibria in two-person zero-sum sequential games with incomplete information and perfect recall (like Texas Hold’em Poker). Our algorithm is numer- ically stable, performs only basic iterations (i.e matvec multiplications, clipping, etc., and no calls to external first-order oracles, no matrix inversions, etc.), and is applicable to a broad class of two-person zero-sum games including simultaneous games and sequential games with incomplete information and perfect recall. The ap- plicability to the latter kind of games is thanks to the sequence-form representation which allows one to encode such a game as a matrix game with convex polytopial strategy profiles. We prove that the number of iterations needed to produce a Nash- equilibrium with a given precision is inversely proportional to the precision. We present experimental results on matrix games on simplexes and Kuhn Poker.

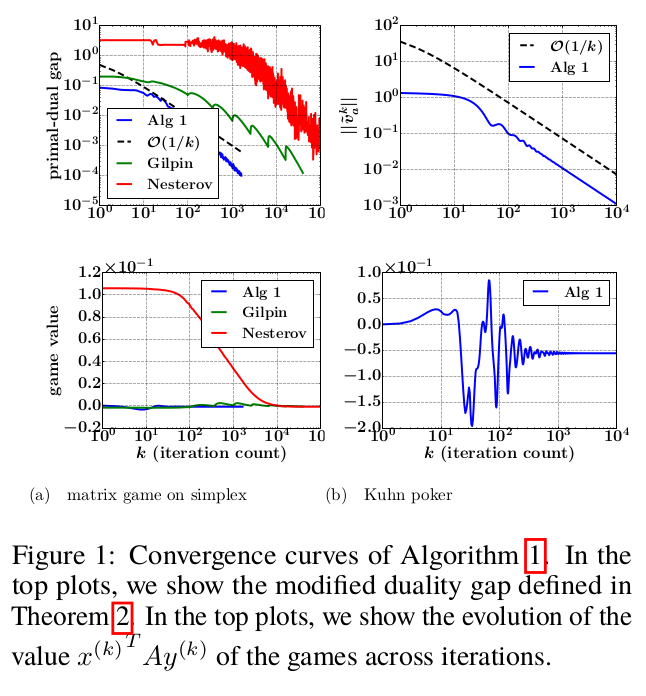
Results

Read the full paper on arXiv.

Concluding remarks

Making use of the sequence-form representation, we have proposed an equivalent Generalized Saddle-Point (GSP) formulation to the Nash-equilibrium problem for sequential games with incomplete information and perfect recall (e.g Texas Hold’em, etc.). Then, we have devised a simple numerically stable primal-dual algorithm for solving the GSP, and so by equivalence, compute (approximate) Nash-equilibria for such games. Our algorithm is simple to implement, with a low constant cost per iteration, and enjoys a rigorous convergence theory with a proven $\mathcal{O}(1/\epsilon)$ convergence in terms of basic operations (matvec products, clipping, etc.), to a Nash $(\epsilon,0)$-equilibrium of the game. On an experimental footing, this is just preliminary works, and in future we plan to run more experiments on real Poker games to measure the practical power of the proposed algorithm compared to state-of-the-art methods like CFR and variants and first-order methods like Andrew Gilpin’s.