\[\def\sign{\operatorname{sign}} \def\qed{\Box} \def\im{\operatorname{im}} \def\grad{\operatorname{grad}} \def\curl{\operatorname{curl}} \def\div{\operatorname{div}} \def\dim{\operatorname{dim}} \def\X{\mathcal X} \def\Y{\mathcal Y} \def\C{\mathcal C} \def\M{\mathcal M} \def\Xstar{\X^\star} \def\Ystar{\Y^\star} \def\Astar{A^\star} \def\BX{\mathbb B_{\X}} \def\BXstar{\mathbb B_{\Xstar}} \def\Xss{\X^{\star\star}} \def\Yss{\Y^{\star\star}} \def\gss{g^{\star\star}} \def\fss{f^{\star\star}} \def\fstar{f^\star} \def\gstar{g^\star} \def\xstar{x^\star} \def\ystar{y^\star} \def\opt{\operatorname{opt}} \def\dom{\operatorname{dom}} \def\conv{\operatorname{conv}} \def\epi{\operatorname{epi}} \def\iff{\;\operatorname{iff}\;} \def\st{\;\operatorname{s.t}\;} \def\softmax{\operatorname{softmax}} \def\kl{\operatorname{KL}} \def\tv{\operatorname{TV}} \def\div{\operatorname{div}} \def\inte{\operatorname{int}} \def\ball{\mathbb B} \def\card{\operatorname{card}} \def\enet{\mathcal N_\epsilon} \def\bP{\mathbb P}\]

I – Introduction

In some theoretical deep learning work I’ve been doing lately, it seems all my problems have an answer hidden somewhere in the rich body of knowledge around random matrices. I had been flirting with this subject for a while, but always at a safe distance. A few weeks ago, I decided to take a deep dive into this subject (Random Matrix Theory, or RMT for short), and my life has been a bit more comfortable ever since…

In this post, I will be interested in the smallest singular-value of a random $N \times n$ matrix $A$ with real coefficients. Believe it or not, such knowledge can be used to understand exploding gradients in certain deepnet architectures (but this is another story, for another day…). The parameter $\lambda := n/N$, usually referred to as the aspect ratio, will play a central role in the proofs. Singular values of $A$ are nothing other than the nonzero eigenvalues of the covariance matrix $AA^T$.

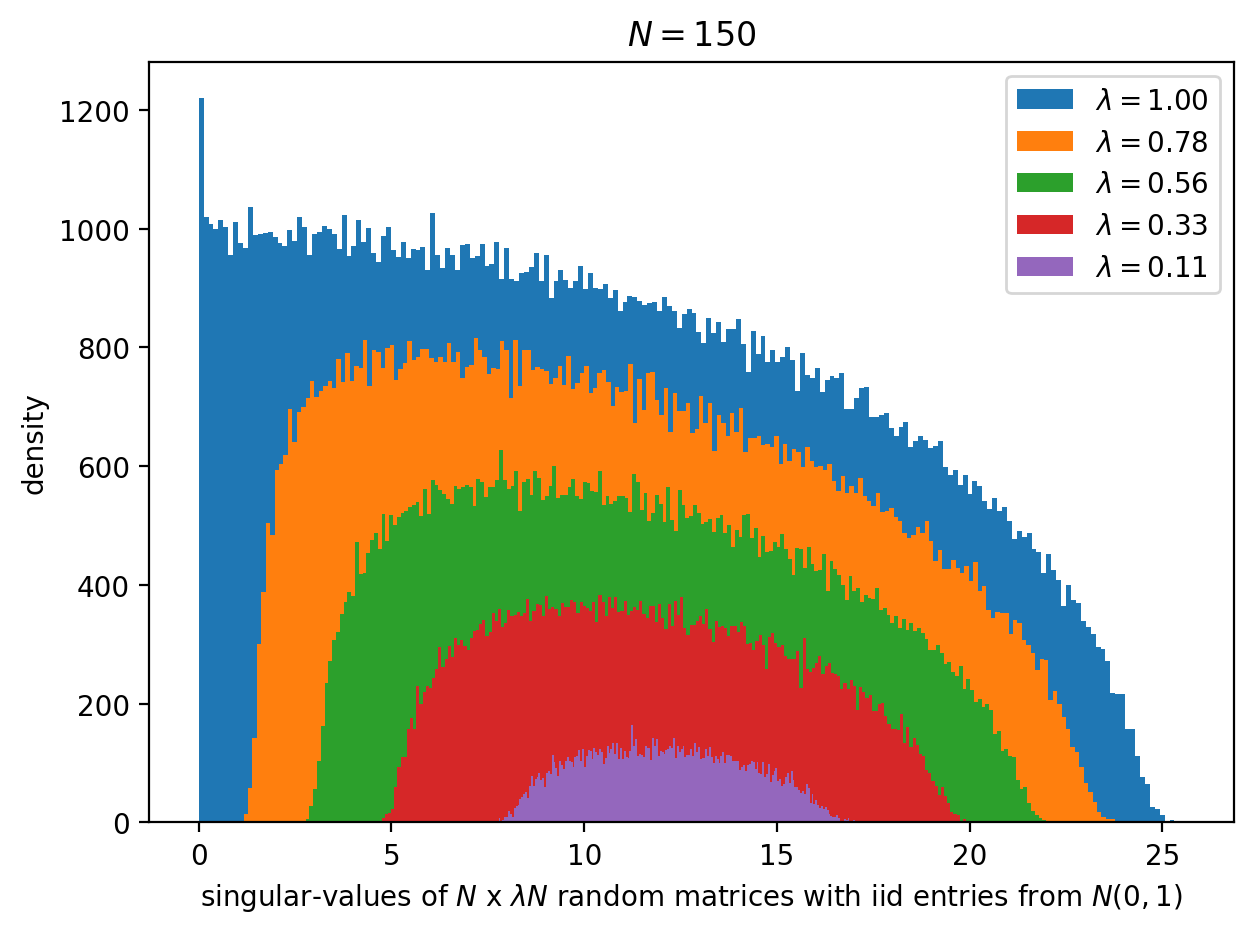
It is well-known if $A$ with entries which are iid zero-mean (together with some moment conditions), then in the limit when $n,N \to \infty$ with $n/N = \lambda \in (0, 1)$, the joint distribution of the eigenvalues of the random psd matrix $AA^T$ is a Marcenko-Pastur law (named after Ukrainian physists Vladimir Marcenko and Leonid Pastur). This result is quite impressive, as it is (1) universal (2) gives the analytic form for the joint distribution. But, we want more! We are unsatisfied with this result for at least two good reasons

  • It is asymptotic!
  • It is asymptotic!

Recall the well-known variational formulae for the largest and the smallest singular-values of $A$, namely

\[\begin{split} s_{\max}(A) &:= \sup_{x \in \mathbb S_{n-1}}\|Ax\|,\\ s_{\min}(A) &:= \inf_{x \in \mathbb S_{n-1}}\|Ax\|, \end{split}\]

where $\mathbb S_{n-1} := \{x \in \mathbb R^n\mid \|x\| = 1\}$ be the unit-sphere in $n$-dimensional euclidean space $\mathbb R^n$. Since $A$ is a random matrix, both $s_{\min}(A)$ and $s_{\max}(A)$ are random variables. We will be interested in non-asymptotic confidence intervals for these quantities.

Prerequisites. Though not strictly necessary, basic vocabulary concerning the stuff I’ll be talking about can be picked up from Roman Vershynin’s High-dimensional probability textbook (google for the pdf file), especially the chapters on covering / packing, and high-dimensional random vectors.

I.1 – Main result

The main result of this post will be the following non-asymptotic result

Theorem 1.1.1 (Rectanglular random matrices have large singular-values.) Let $N$ and $n$ be positive integers with $n/N =: \lambda \in (0, 1)$, and let $A$ be an $N\times n$ random matrix with iid entries from $\mathcal N(0,1)$. For every $C>0$, there exists $c>0$ depending on $\lambda$ and $C$ such that $s_{\min}(A) \ge c\sqrt{N}$ w.p $1-2e^{-CN}$.

A few important points to note:

  • What is striking about the above theorem is that it works for all $C>0$. In contrast, a version of this theorem with a perculiar value of $C$ is not hard to get (e.g see Roman Vershynin text book); a bound which works for arbitray $C>0$ is much more difficult to obtain. Such a bound has the distinctive advantage that it can be used to absorb large entropy costs associated with union bounds over events such as the one in the theorem. This trick will be played in the proof of Corollary 1.1.1 below.

  • A careful inspection of the proof of this theorem (given further below) reveals that we can replace the base distribution $\mathcal N(0,1)$ of the coefficients of $A$ by any symmetric unit-variance $\sigma^2$-subGaussian such that $0 \le \sigma \le 1$.

Definition 1.1.1 (Gaussian tails). A zero-mean random variable $\zeta$ on $\mathbb R$ is called $\sigma^2$-subGaussian if there exists a constant $A>0$ such that \(\mathbb \bP(|\zeta| \ge t) \le Ae^{-t^2/(2\sigma^2)},\;\forall t \ge 0.\)

Thus the tails of a subGaussian random variable compare to that of a Gaussian of same variance. Usual examples include Gaussian / normal random variables; bounded random variables; etc. The following result will be crucial in the sequel.

For $I \subseteq [N]$ with $|I| = k$, let $A_I$ be the $k \times n$ submatrix obtained from $A$ by only considering row indices which are in $I$. The following corollary says that with overwhelming probability, all sufficiently rectangle submatrices of a rectangular random matrix of the type in Theorem 1.1.1 above, have smallest singular-value of size $\Omega(1)\sqrt{N}$. Viz,

Corollary 1.1.1 (Almost all rectangular submatrices of a rectangular random matrix have large singular-values). Let the random matrix $A$ be as in Theorem 1.1.1. For every $p \in (\lambda, 1]$, there exists $c > 0$ depending only on $\lambda$ and $p$ such that w.p $1-o(1)$, it holds that $s_{\min}(A_I) \ge c\sqrt{N}$ for every $I \subseteq [N]$ with $|I| \ge pN$.

Proof of Corollary 1.1.1. Let $C>0$ be arbitrary. Denote by $\mathcal I_k$ the collection of all subsets of $[N]$ with exactly $k$ elements, and let $\mathcal I := \cup_{k \ge pN}\mathcal I_k$. Note that $|\mathcal I| = \sum_{k=\lceil pN\rceil}^N{N\choose k}$. It is well-known that

\[\sum_{k=\lceil pN\rceil}^N{N\choose k} \le e^{H(p)N}, \tag{1}\]

where $H(p) := -p\log(p) - (1-p)\log(1-p) \in (0,\log(2))$ is the natural / naperian entropy of $p$. Now, let $I \in \mathcal I$ with $|I| = k \ge pN$. Because the submatrix $A_I$ has aspect ratio $n/k \le n/(pN) = \lambda/p \in (0, 1)$, we may apply Theorem 1.1.1 to guarantee the existence of $c_k>0$ depending only on $\lambda$, $p$, $k$, and $C$ such that

\[\bP(s_{\min}(A_I) < c_k\sqrt{pN}) \le \bP(s_{\min}(A_I) < c_k\sqrt{k}) \le 2e^{-Ck} \le 2e^{-CpN}.\]

Let $c := \sqrt{p}\min_k c_k$. A simple union bound (see Exercise 1.2.2 below) then gives

\[\begin{split} \bP(\exists I \in \mathcal I \text{ s.t }s_{\min}(A_I) < c\sqrt{N}) &\le |\mathcal I| \cdot \max_{I \in \mathcal I}\bP(s_{\min}(A_I) < c\sqrt{N})\\ &\le |\mathcal I| \cdot \max_{I \in \mathcal I}\bP(s_{\min}(A_I) < c_{|I|}\sqrt{pN})\\ &\le |\mathcal I| \cdot 2e^{-CpN} \le e^{H(p)N}\cdot 2e^{-CpN}\\ &\le 2e^{-(Cp-H(p))N}. \end{split}\]

The result then follows upon taking any $C > H(p)/p > 0$. $\quad\quad\quad\qed$

I.2 – Exercises

Exercise 1.2.1 (Entropy and counting). Prove the bound (1). Hint: Make connection to binomial distribution.

Exercise 1.2.2 (The “union bound”). Prove that if $E_1,\ldots,E_k$ are events on the same space, then $\bP(\cup_{i=1}^k E_i) \le k\max_{i=1}^k \bP(E_i)$.

Exercise 1.2.3 (Volume-packing). Prove that the number of balls in $\mathbb R^k$ of radius $1/2$ which can be enclosed in $\mathbb S_{k-1}$ is at most $6^k$.

II – Main ingredients

Let $(\mathcal X,d)$ be a (pseudo-)metric space, $S \subseteq \mathcal X$, and $\epsilon > 0$. A subset $\mathcal N \subseteq S$ is called an $\epsilon$-net for $S$ if every point of $S$ is withing a distance of $\epsilon$ from a point of $\mathcal N$. That is, $S \subseteq \cup_{z \in \mathcal N}\ball(z;\epsilon)$, where $\ball(z;\epsilon) := \{x \in \mathcal X \mid d(x,z) \le \epsilon\}$ is the ball of radius $\epsilon$ centered at $z$. An $\epsilon$-net is called maximal if it is maximal w.r.t set inclusion. By Zorn’s Lemma, such a net always exists. The cardinality of an maximal $\epsilon$-net for $S$ is called the $\epsilon$-covering number of $S$.

Lemma 2.1 (Upper-bound for covering number). For every $\epsilon \in (0, 1)$, we have the bound $| \enet(\mathbb S_{k-1})| \le (3/\epsilon)^k$. More generally, if $S$ is a nonempty centrally-symmetric subset of $(\mathbb R^k,\ell_2)$, then $| \enet(S) | \le \mathcal (\alpha/\epsilon)^k$, for some constant $\alpha$ which is independent of $k$.

The proof is standard and can be carried out via a volume-packing argument and is left as an exercise (Hint: workout Exercise 1.2.3 of the previous section).

For any positive integer $k$, let $\mathbb B_k := \{x \in \mathbb R^k \text{ s.t } \|x\| \le 1\}$ be the unit-ball in $k$-dimensional euclidean space $\mathbb R^k$ and let $\mathbb S_{k-1} := \{x \in \mathbb R^k \text{ s.t } \|x\| = 1\}$ be the corresponding unit-sphere.

The following two facts will be crucial for the proof of the main result above.

Fact 2.1 (Gaussian small-ball probability). If $X = (X_1,\ldots,X_k) \sim \mathcal N(0,I_k)$, then there exists $C_1>0$ such that $\bP(\|X\| \le u \sqrt{k}) \le (C_1u)^k$ for all $u \ge 0$.

Proof. $\bP(\|X\| \le u \sqrt{k}) = (2\pi)^{-k/2}\int_{u\sqrt{k}\mathbb B_k}e^{-\|x\|^2}dx \le (2\pi)^{-k/2}\mbox{vol}(u\sqrt{k}\mathbb B_k) \le (C_1u)^k$, for some $C_1>0$ (which can be made explicit).

Fact 2.2 (Spectral-norm upper bound). For every $C>0$, there exists $C_0>0$ such that $s_{\max}(A) \le C_0\sqrt{N}$ w.p $1-e^{-CN}$.

Proof. See Fact 2.4 of this paper by Litvak, Pajor, and Rudelson.

III. – Proof of the main claim (Theorem 1.1.1)

We are now ready to proof the main claim.

Proof of Theorem 1.1.1. Let $\epsilon \in (0, 1)$, to be prescribed later, and let $\enet$ be a maximal $\epsilon$-net for $\mathbb S_{n-1}$. By Lemma 2.1, we have $| \enet | \le (3/\epsilon)^n = (3/\epsilon)^{\lambda N}$. Now, for each $x \in \mathbb S_{n-1}$, there exists $z \in \enet$ such that $\|x-z\| \le \epsilon$. Writing $Ax = Az + A(x -z)$, the triangle inequality gives

\[\|Ax\| \ge \|Az\| - \|A(x-z)\| \ge \|Az\|-\epsilon s_\max(A).\]

Minimizing both sides, we obtain

\[s_\min(A) = \inf_{x \in \mathbb S_{n-1}}\|Ax\| \ge \min_{z \in \enet}\|Az\|-\epsilon s_\max(A).\]

Let $C_1$ be as in Fact 2.1 with $k=N$. For arbitrary $C>0$, let $C_0$ be as in Fact 2.2 with $k=N$, and let $c > 0$, to be carefully chosen later. By the above inequality, we know that for all $z \in \enet$, \begin{eqnarray} (s_\max(A) \le C_0\sqrt{N} \text{ and } \|Az\| \ge 2c \sqrt{N}) \implies s_\min(A) \ge 2c\sqrt{N}-\epsilon C_0\sqrt{N} \ge c\sqrt{N}, \tag{2} \end{eqnarray}

provided $\epsilon = c/C_0$ with $c < C_0$. Thus, one computes

\[\begin{split} \bP(s_\min(A) < c\sqrt{N}) &= \bP(s_\min(A) < c \sqrt{N},s_\max(A) > C_0\sqrt{N})\\ &\quad\quad\quad + \bP(s_\min(A) > C_0\sqrt{N},s_\max(A) \le C_0\sqrt{N})\\ &\le \bP(s_\max(A) > C_0\sqrt{N}) + \bP(s_\min(A) < c \sqrt{N},s_\max(A) \le C_0\sqrt{N})\\ & \le e^{-CN} + \bP(\min_{z \in \enet}\|Az\| < 2c\sqrt{N}), \text{ by Fact 2 and inequality (2)}\\ &\le e^{-CN} + | \enet |\cdot\max_{z \in \enet}\bP(\|Az\| < 2c\sqrt{N}),\text{ by a union-bound}\\ & \le e^{-CN} + (3/\epsilon)^n(C_1 \cdot 2c)^N \le e^{-CN}+((3/\epsilon)^\lambda\cdot C_1\cdot 2c)^N\\ &\le e^{-CN} + (2C_1(3C_0)^\lambda c^{1-\lambda})^N \le e^{-CN} + e^{-CN}=2e^{-C N}, \end{split}\]

for sufficiently small $c \in (0,C_0)$ such that $2C_1(3C_0)^\lambda c^{1-\lambda} < e^{-C}$.

Therefore, given arbitrary $C>0$, the bound $\bP(s_\min(A) \le c\sqrt{N}) \le 2e^{-CN}$ is guaranteed by taking $c \in (0,c_\lambda(C))$, where \(\begin{split} c_\lambda(C) := \min(C_0,(2C_1e^C(3C_0)^\lambda)^{\frac{-1}{1-\lambda}})>0. \end{split} \tag{3}\)

This completes the proof of the claim. $\quad\quad\Box$

To be continued…

IV. – References

  • Introduction to the non-asymptotic analysis of random matrices, by Roman Vershynin
  • Topics in random matrix theory, by Terence Tao

  • Recent developments in non-asymptotic theory of random matrices, by Mark Rudelson