\[\def\sign{\operatorname{sign}} \def\qed{\Box} \def\im{\operatorname{im}} \def\grad{\operatorname{grad}} \def\curl{\operatorname{curl}} \def\div{\operatorname{div}} \def\dim{\operatorname{dim}} \def\X{\mathcal X} \def\Y{\mathcal Y} \def\C{\mathcal C} \def\M{\mathcal M} \def\Xstar{\X^\star} \def\Ystar{\Y^\star} \def\Astar{A^\star} \def\BX{\mathbb B_{\X}} \def\BXstar{\mathbb B_{\Xstar}} \def\Xss{\X^{\star\star}} \def\Yss{\Y^{\star\star}} \def\gss{g^{\star\star}} \def\fss{f^{\star\star}} \def\fstar{f^\star} \def\gstar{g^\star} \def\xstar{x^\star} \def\ystar{y^\star} \def\opt{\operatorname{opt}} \def\dom{\operatorname{dom}} \def\conv{\operatorname{conv}} \def\epi{\operatorname{epi}} \def\iff{\;\operatorname{iff}\;} \def\st{\;\operatorname{s.t}\;} \def\softmax{\operatorname{softmax}} \def\kl{\operatorname{KL}} \def\tv{\operatorname{TV}} \def\div{\operatorname{div}} \def\inte{\operatorname{int}} \def\ball{\mathbb B} \def\card{\operatorname{card}} \def\enet{\mathcal N_\epsilon} \def\bP{\mathbb P}\]

I – Introduction

Consider a two-layer neural network on $d$-dimensional inputs, $k$ hidden neurons, activation function $\sigma:\mathbb R \to \mathbb R$, and one scalar output. Let the weights of each each hidden neuron $w_1,\ldots,w_k$ be sampled independently and uniformly from the unit-sphere in $\mathbb R^d$, and collected into a $k \times d$ random matrix $W$. Consider a sample of $n$ data points $x_1,\ldots,x_n$ independent of one another and of the weights matrix $W$, sampled independently and uniforml on the same sphere, and collected into an $n \times d$ random matrix $X$. Form the random $n \times k$ matrix $Z$ with entries $z_{aj} := \sigma(x_a^\top w_j)$, for some $1$-homogeneous continuous function $\sigma:\mathbb R \to \mathbb R$.

Goal. In this post, we are interested good probabilitistic upper-bounds on the largest eigenvalue of the $n \times n$ gram matrix $ZZ^\top$.

Now, we may write $ZZ^\top = \sum_{j=1}^k G_j$, where $G_j := \sigma(Xw_j) \otimes \sigma(Xw_j) \in \mathbb R^{n \times n}$, where $\sigma(Xw_j) := (\sigma(x_1^\top w_j),\ldots,\sigma(x_n^\top w_j)) \in \mathbb R^n$. Set $\overline{G}_j := G_j - \mathbb E_W[G_j]$. Note that thedue to $1$-homogeneity of the activaiton function $\sigma$, it is a direct consequence of Lemma 2.2.2 of Buchweitz (2016) that the $(a,b)$ entry of $\mathbb E[G_j]$ is given by

\[(\mathbb E[G_j])_{a,b} = \mathbb E_{w_j}[\sigma(x_a^\top w_j)\sigma(x_b^\top w_j)] = \frac{1}{d}\phi(x_a^\top x_b), \tag{*}\]

for some $\phi:\mathbb R \to \mathbb R$ which is continuous on $(-1, 1]$ which is independent of $n$, $d$, and $k$. In particular the matrix $\mathbb E_{w_j} [G_j]$ is independent of the index $j \in [k]$. We will prove the following result

Main claim. Let $\Phi := (1/k)ZZ^\top$ and $\overline{\Phi} := \mathbb E_W[\Phi]$. For sufficiently large $n$, $d$, and $k$ such that $n=\mathcal O(d)$ and $k \gg \log d$, the following hold w.p $1-d^{-\Omega(1)}$ over $X$ and $W$.

  • Concentration of entier eigenspectrum of normalized gram matrix: \(\|\Phi-\overline{\Phi}\|_{op} \le \sqrt{\dfrac{\log d}{k}}.\)
  • Upper-bound on largest eigenvalue: \(\lambda_{\max}(\Phi) \le \begin{cases}\mathcal O(\max(\sqrt{\dfrac{\log d}{k}},\dfrac{1}{d})),&\mbox{ if }\phi\text{ is }\mathcal C^3\text{ at }0\text{ and }\phi(0) = 0,\\ \mathcal O(1),&\mbox{else.}\end{cases}\)

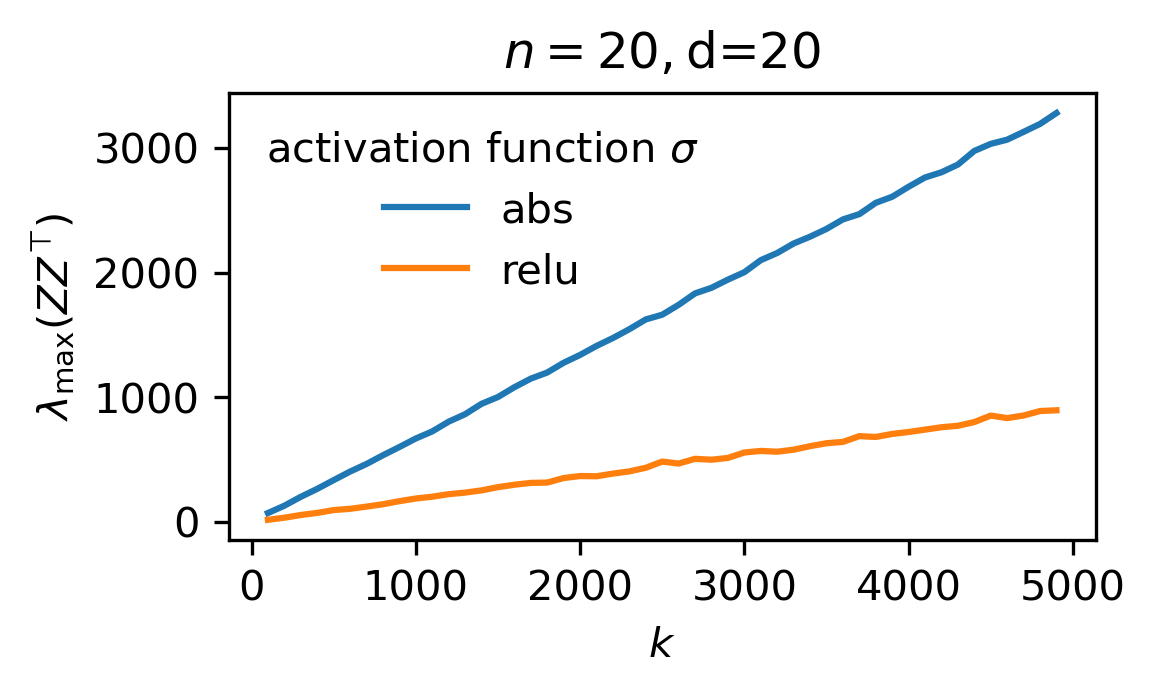
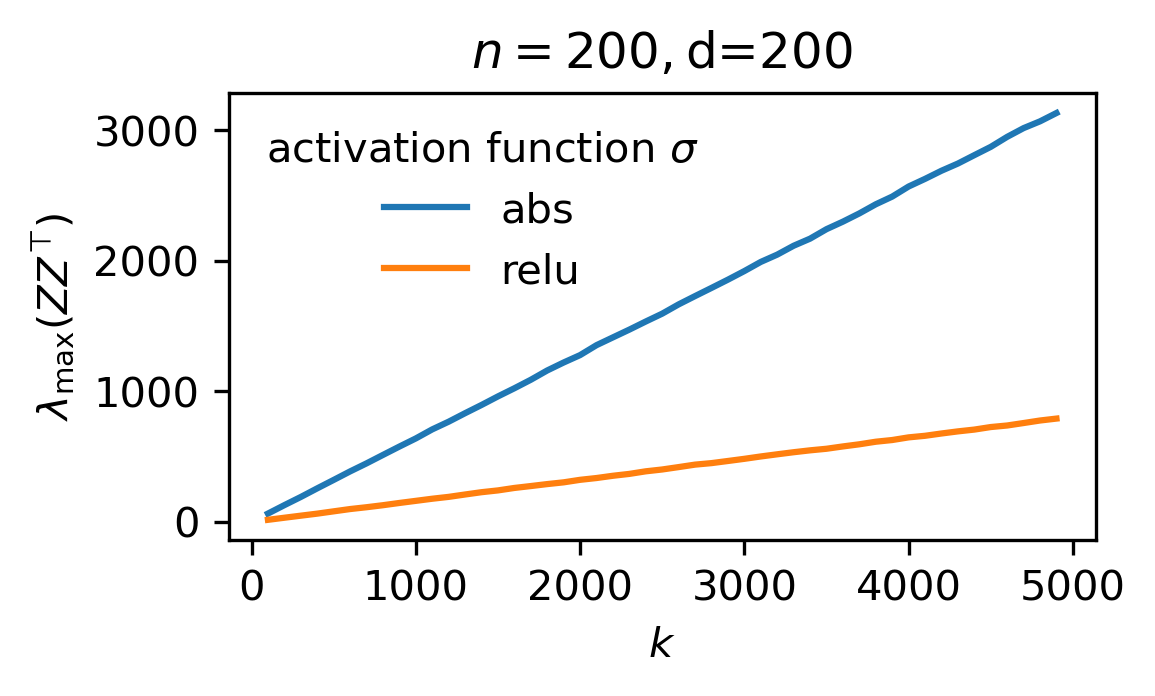
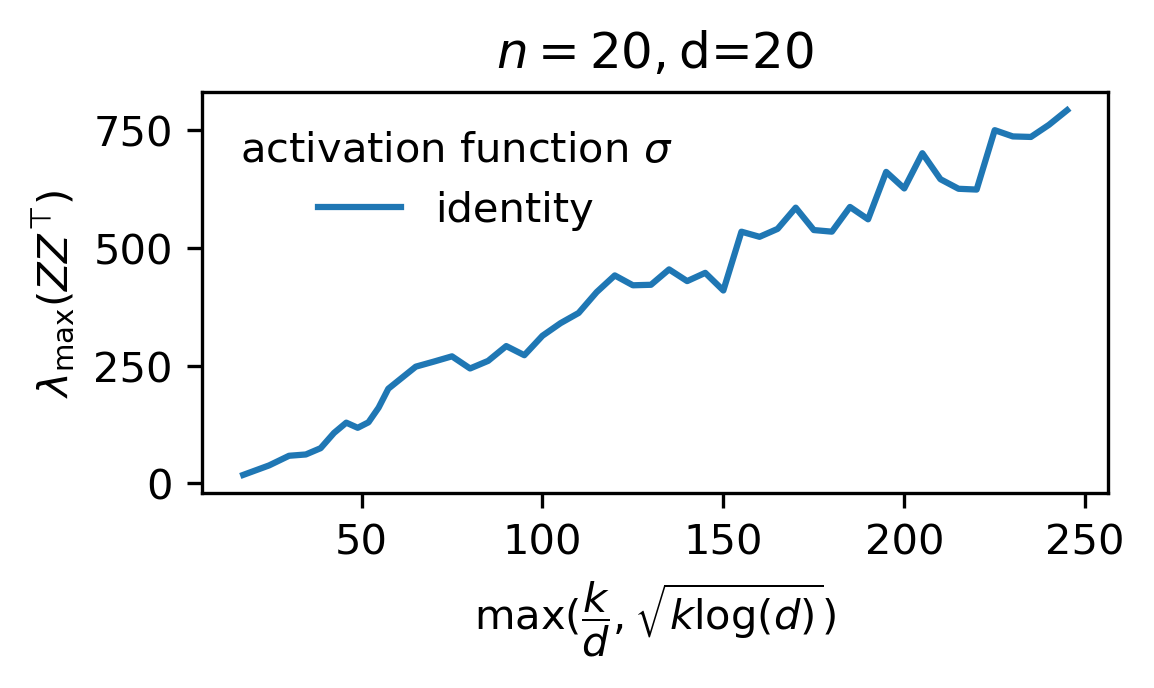
II – Proof (of main claim)

The proof is subdivided into sevral pieces, for the reader’s (and the writer’s!) convenience.

(1) Uniform upper-bound for spectral norm of the individual $G_j$’s. Standard RMT (see references at the end of this post) tells us that except on an event $\mathcal E$ which occurs w.p $1-e^{-\Omega(1)}$ or less, one has

\[\|X\|_{op} = \mathcal O(1)\text{ w.p }1-e^{-\Omega(d)}. \tag{2}\]

Now, \(\|\overline{G}_j\|_{op} \le \|G_j\|_{op} + \|\mathbb E_{w_j}[G_j]\|_{op}\), and conditioned on the compliment $\mathcal E’$ of the event $\mathcal E$, one can bound \(\begin{split} \|G_j\|_{op} = \|\sigma(Xw_j)\|^2 &\le \sum_{a=1}^n (x_a^\top w_j)^2 = \|Xw_j\|^2 \le \|X\|_{op}^2 = \mathcal O(1). \end{split}\)

On the other hand, \(\|\mathbb E_{w_j}[G_j]\|_{op} = (1/d)\|\phi(XX^\top)\|_{op} = \mathcal O(n/d)=\mathcal O(1)\). Combining with the previous inequality gives \(\|\overline{G}_j\|_{op} = \mathcal O(1)\).

(2) Upper-bound for pseudo-variance. For simplicity, let $\phi_{ab} := \phi(x_a^\top x_b)$ and recall from (*) that $\mathbb E_{w_j}[z_{aj}z_{bj}] = (1/d)\phi_{ab}$. The $(a,b)$ entry of $\mathbb E_{w_j}[\overline{G_j}^2]$ writes

\[\begin{split} \mathbb E_{w_j}[(\overline{G_j}^2)_{a,b}] &= \sum_{c=1}^n \mathbb E_{w_j}[(\sigma(x_a^\top w_j)\sigma(x_c^\top w_j)-\frac{\phi_{ac}}{d})(\sigma(x_b^\top w_j)\sigma(x_c^\top w_j)-\frac{\phi_{bc}}{d})]\\ &= \sum_{c=1}^n \mathbb E_{w_j}[z_{aj}z_{bj} z_{cj}^2-z_{aj}z_{cj}\frac{\phi_{bc}}{d}-z_{bj}z_{cj}\frac{\phi_{ac}}{d}+\frac{\phi_{ac}\phi_{bc}}{d^2}]\\ &= \sum_{c=1}^n \mathbb E_{w_j}[z_{aj}z_{bj}z_{cj}^2] - \frac{\phi_{ac}\phi_{bc}}{d^2} = \sum_{c=1}^n \mathbb E_{w_j}[z_{aj}z_{bj}z_{cj}^2] - \mathcal O(\frac{n}{d^2}). \end{split} \tag{3}\]

Thus, \(|\mathbb E_{w_j}[(\overline{G_j}^2)_{a,b}]| \le \mathcal O(1/d) + \sum_c \mathbb E_{w_j}[|z_{aj}z_{bj}|z_{cj}^2] \le \mathcal O(1/d) + \mathbb E_{w_j}[|z_{aj}z_{bj}|\sum_{c=1}^n z_{cj}^2]\). By Cauchy-Schwarz inequality, we have

\[(\mathbb E_{w_j}[|z_{aj}z_{bj}|\sum_{c=1}^n z_{cj}^2])^2 \le \mathbb E_{w_j}[z_{aj}^2 z_{bj}^2]\mathbb E_{w_j}[(\sum_{c=1}^n z_{cj}^2)^2].\]

We bound each factor on the rightmost side like so:

  • \(\mathbb E_{w_j}(\sum_{c=1}^n z_{cj}^2)^2 \le \mathbb E_{w_j}[(\sum_{c=1}^n (x_c^\top w_j)^2)^2] = \mathbb E_{w_j}\|Xw_j\|^4 \le \|X\|^4_{op} = \mathcal O(1)\) on the event $\mathcal E’$, and
  • \(\mathbb E_{w_j}[z_{aj}^2z_{bj}^2] \le \|\phi\|_\infty ^2 \mathbb E_{w_j}[(x_a^\top w_j)^2(x_b^\top w_j)^2] = \|\phi\|_\infty^2\dfrac{(x_a^\top x_b)^2}{d(d+2)} \le \mathcal O(\dfrac{1}{d^2})\).

Combining with (3) gives \(\sup_{a,b \in [n]}|\mathbb E_{w_j}[(\overline{G_j}^2)_{a,b}]| \le \mathcal O(1/d)\) on the event $\mathcal E’$, and so \(v(ZZ^\top):= \sum_{j=1}^k \|\mathbb E_{w_j}[(\overline{G_j}^2)\|_{op} \le k \sup_{j=1}^k \|\mathbb E_{w_j}[\overline{G_j}^2]|\|_{op} \le k \cdot \mathcal O(n/d) = \mathcal O(k)\) on the same event.

(3) Matrix Bernstein inequality. By the matrix Bernstein inequality (see Tropp 2015), we obtain that conditioned on $\mathcal E’$, it holds with probability $1-\delta$ for $\delta = d^{-c}$ that,

\[\begin{split} \|\frac{1}{k}ZZ^\top - \mathbb E_{w_1}[G_1]\|_{op} &\le \sqrt{\frac{1}{k^2}v(ZZ^\top)\log d} + \mathcal O(\frac{1}{k}\log d)\\ &\lesssim \sqrt{\frac{1}{k}\log d} + \frac{1}{k}\log d \lesssim \sqrt{\frac{\log d}{k}}. \end{split} \tag{4}\]

This proves the first part of the claim upon recalling that the “bad” event $\mathcal E$ only occurs with probability at most $d^{-\Omega(1)}$.

For the second part thanks to Proposition A.2 of Liang and Rakhlin (2018), we observe that

\[\|\mathbb E_{w_1}[G_1]\|_{op} = \dfrac{1}{d}\|\phi(XX^\top)\|_{op} \le \begin{cases} \dfrac{1}{d}\mathcal O(1)=\mathcal O(\dfrac{1}{d}),&\mbox{ if }\phi\text{ is "awful"},\\ \dfrac{1}{d}\mathcal O(n)=\mathcal O(\dfrac{n}{d})=\mathcal O(1),&\mbox{ else.} \end{cases}\]

Thus, taking $t = (\log d)^c$ in (4) for an appropriate $c>0$, one gets the result, after recalling that $\mathcal E$ occurs w.p at most $d^{-\Omega(1)}$, the claim follows $\quad\quad\Box$.

III – References

  • Introduction to the non-asymptotic analysis of random matrices, by Roman Vershynin.
  • Topics in random matrix theory, by Terence Tao.
  • Recent developments in non-asymptotic theory of random matrices, by Mark Rudelson.
  • An Introduction to Matrix Concentration Inequalities, by Joel Tropp (2015).
  • Concentration of functions beyond lévy’s inequality, by Erez Buchweitz (2016).
  • Just Interpolate: Kernel “Ridgeless” Regression Can Generalize, Liang and Rakhlin (2018).